Основные построения золотого сечения — Записки недизайнера — LiveJournal
На практике при выборе формата листа (картины) часто используют «классические» пропорции сторон прямоугольника, в котором отношение меньшей стороны к большей составляет число 0,6180339, а большей к меньшей — 1,6180339. Эти числа с древнейших времён называют золотыми, а отношение величин, необходимое для их получения, известно как золотая пропорция или золотое сечение.
Основа учения о гармонии мира, выраженная в числовых отношениях, была заложена древнегреческим учёным-математиком Пифагором (VI в до н.э). Им представлено золотое сечение как одна из закономерностей, математически точно определяющая наиболее красивое и гармоничное соотношение частей целого, разделённого на две неравные половины.
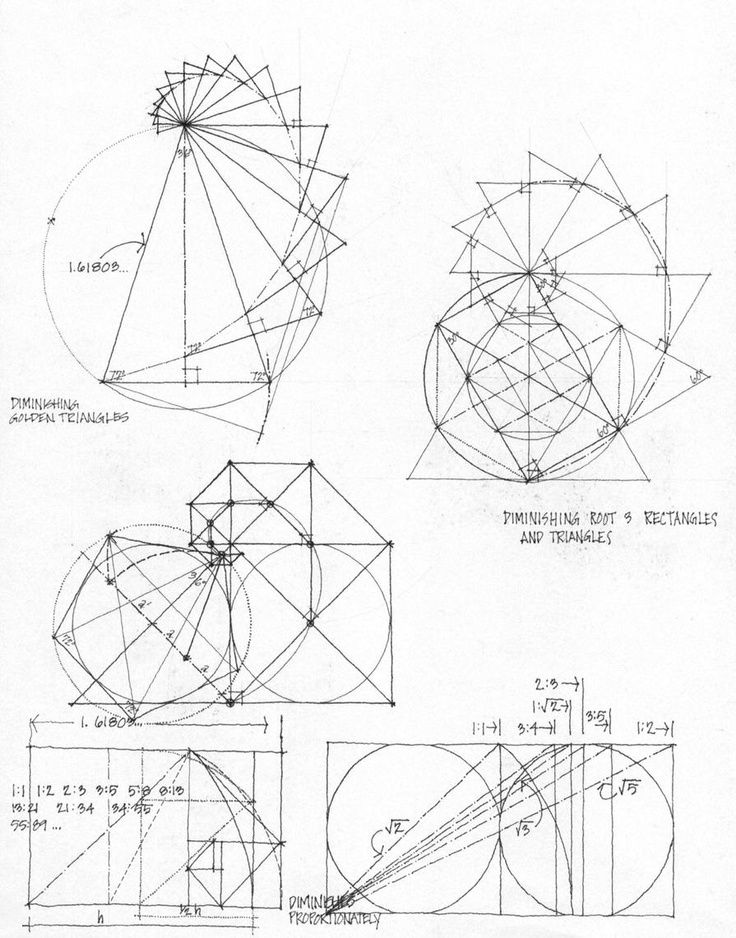
На соотношении частей отрезка в пропорциях золотого сечения основано построение прямоугольника. С помощью диагоналей осуществляется членение его на составные части, при котором образуется динамика пропорциональных фигур — квадрата, прямоугольника, а также прямоугольного и равнобедренного треугольников.
Т.о., используя диагонали можно получить последовательный ряд увеличивающихся прямоугольников, с соотношением сторон — 1:√ 2, 1:√3, 1:√4, 1:√5, производных от квадрата.
При стороне √4 образуется прямоугольник с удвоенным квадратом. При стороне √3 образуется два прямоугольных треугольника, у которых общая гипотенуза является диагональю прямоугольника, равная удвоенной величине меньшего катета (т.е. стороне квадрата), и они имеют острые углы 30 и 60 градусов.
Диагональ используется и в построении последовательно увеличивающихся квадратов, создающих «динамическое» развитие их величины.
В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне. Эти преобразования иногда называют «активным квадратом».
Геометрическая система динамических пропорций квадрата, прямоугольника и треугольника были основой в создании архитектурных сооружений в ранний период Древнего Египта. Кроме того, в условиях примитивной техники архитектурного строительства в те далёкие времена постоянно требовалось восстановление перпендикуляра к прямой, которое осуществлялось тогда при помощи верёвки с 12 узлами.
С древнейших времён золотое сечение используется в практике построения различных изображений. Это способствует созданию гармоничных образов и уравновешенности пропорций во всём, что на окружает. Пропорции золотого сечения присутствуют в мамематике, и особенно в геометрии, в изобразительном искусстве, в быту и в природе, в растительном и животном мире.
Золотое сечение получило широкое развитие в математике. Так, в XVI веке итальянский учёный Фибоначчи выстроил математический ряд цифр, при котором последующее число определяет сумму двух предыдущих — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Кроме того, устанавливается и другая зависимость этих чисел, при которой отношение каждого последующего к предыдущему выражается числом 1,618.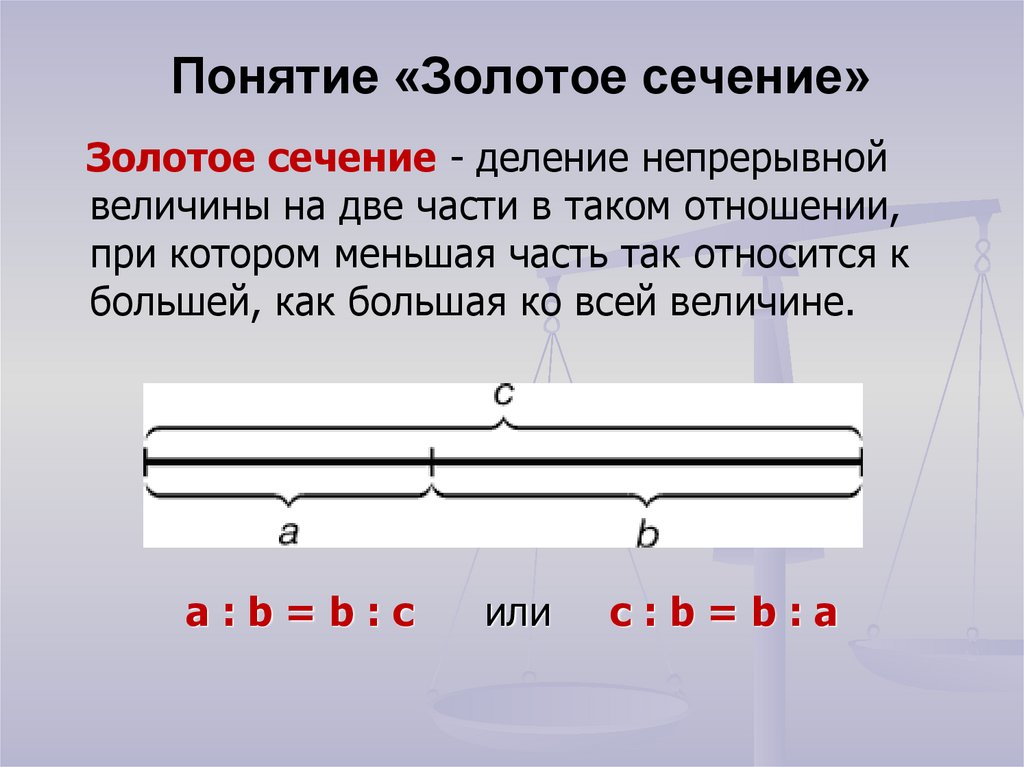 .., а предыдущего к последующему — 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
.., а предыдущего к последующему — 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
Особенно часто золотое сечение используется в геометрии при делении окружности на равные части и построении правильных многоугольников.
В звёздчатом многоугольнике — пятиконечной звезде, каждая точка пересечения её сторон делит их на две неравные части в пропорциях золотого сечения.
С древнейших времён золотое сечение применялось в различных видах изобразительного искусства — в архитектуре, вкульптуре, живописи. Парфенон — классический пример применения золотого сечения в архитектуре.
Особенно широко использовал в своём творчестве соотношение величин золотого сечения Леонардо да Винчи, которое он назвал «божественная пропорция».
Числовой гармонии золотого сечения подчиняются также античные статуи греческого искусства, отражающие пропорции идеально сложённого человеческого тела.
Золотое сечение применяют в начертании букв и цифр различного шрифта.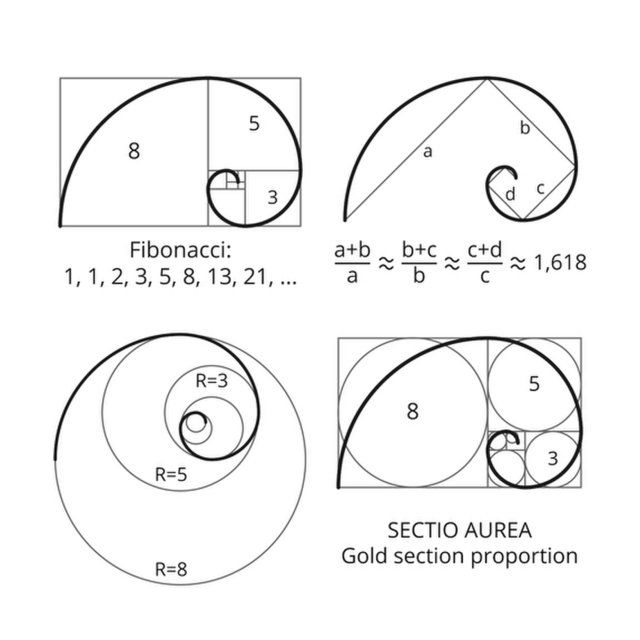
Золотое сечение часто используют в определении величины прямоугольника при заданной его большей или меньшей стороне. Если у прямоугольной картины задана длина (АВ), то её высоту (АС) определяют следующим построением:
Сначала из конца отрезка (В) проводят дугу, равную его половине до пересечения с перпендикуляром (АО=ОВ=ВД). Полученную точку Д соединяют прямой с другим концом отрезка (А). Затем из точки Д проводят дугу радиусом ВД до пересечения с этой прямой и отмечают точку Е. Дуга, проведённая из конца отрезка А радиусом АЕ определяет по вертикальной прямой точку С и искомую высоту картины АС.
Если задана высота картины (АС), то её длину (АВ) определяют другим построением. Сначала строят квадрат АСДЕ со стороной равной АС. Затем из середины стороны квадрата (О) проводят дугу радиусом ОД и получают на горизонтальной прямой точку В, которая определит искомую длину стороны прямоугольной картины АВ.
По прямоугольнику с золотыми пропорциями можно построить любой величинны подобный формат листа.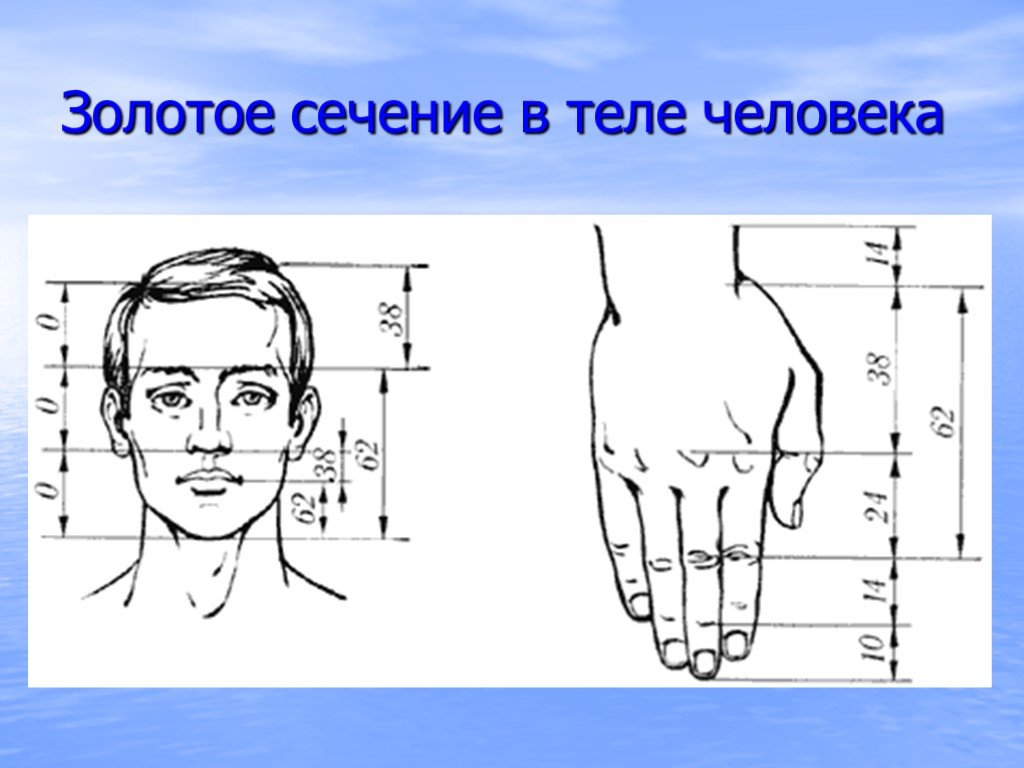
Для этого его накладывают на лист бумаги в один из его углов (А) и проводят в нём диагональ. Затем от точки А откладывают заданный размер горизонтальной или вертикальной стороны формата листа и через его конец проводят перпендикуляр до пересечения с диагональю, которая определит вторую сторону прямоугольника.
Источник: М.Н. Макарова «Практическая перспектива»
Tags: Золотое сечение
Руководство по эксплуатации: Золотое сечение
Золотое сечение – это простой принцип, который поможет сделать дизайн приятным для визуального восприятия. В этой статье мы подробно расскажем как и зачем его использовать.
Распространенная в природе математическая пропорция, называемая Золотое сечение, или Золотая середина, основана на Последовательности Фибоначчи (о которой вы, скорее всего, слышали в школе, или читали в книге Дэна Брауна «Код да Винчи»), и подразумевает под собой соотношение сторон 1:1,61.
Такое соотношение сплошь и рядом встречается в нашей жизни (ракушки, ананасы, цветы и т.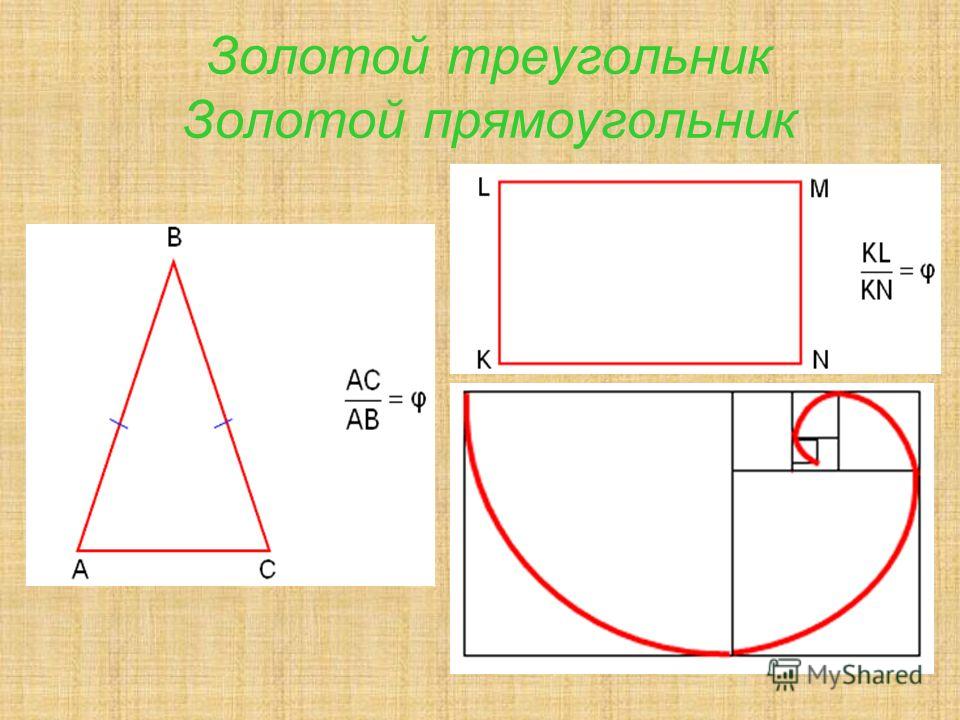 д.) и поэтому воспринимается человеком как нечто естественное, приятное взгляду.
д.) и поэтому воспринимается человеком как нечто естественное, приятное взгляду.
Считается, что Золотое сечение используется человечеством в искусстве и дизайне уже более 4 тысяч лет, а возможно даже больше, если верить ученым, которые утверждают, что древние Египтяне использовали этот принцип при строительстве пирамид.
Знаменитые примеры
Как мы уже говорили, Золотое сечение можно видеть на протяжении всей истории искусства и архитектуры. Вот некоторые примеры, которые только подтверждают обоснованность использования этого принципа:
Архитектура: Парфенон
В древнегреческой архитектуре Золотое сечение использовалось для вычисления идеальной пропорции между высотой и шириной здания, размеров портика, и даже расстояния между колоннами.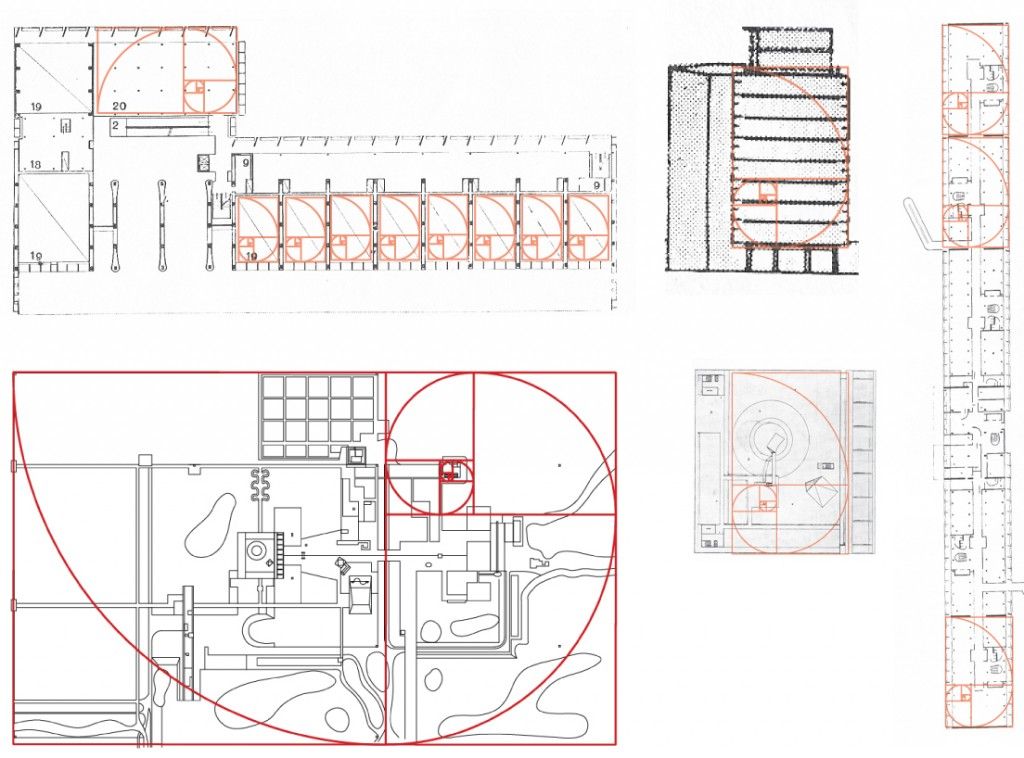 В дальнейшем, этот принцип был унаследован архитектурой неоклассицизма.
В дальнейшем, этот принцип был унаследован архитектурой неоклассицизма.
Искусство: Тайная вечеря
Для художников композиция – основа основ. Леонардо да Винчи, как и многие другие художники, руководствовался принципом Золотого сечения: в Тайной Вечере, к примеру, фигуры учеников расположены в нижних двух третях (большее из двух частей Золотого сечения), а Иисус помещен строго по центру между двумя прямоугольниками.
Веб-дизайн: редизайн Twitter в 2010
Креативный директор Twitter Дуг Боуман (Doug Bowman) опубликовал скриншот в своем аккаунте Flickr, объясняя использование принципа Золотого сечения для редизайна 2010 года. «Все, кто интересуется #NewTwitter пропорциями – знайте, все сделано не просто так», сказал он.
Apple iCloud
Иконка сервиса iCloud тоже совсем не случайный набросок. Как объяснил Такамаса Мацумото в своем блоге (оригинальная японская версия здесь) все построено на математике Золотого сечения, анатомию которого можно увидеть на рисунке справа.
Как построить Золотое сечение?
Построение происходит довольно просто, и начинается с основного квадрата:
Нарисуйте квадрат. Это сформирует длину “короткой стороны” прямоугольника.
Разделите квадрат пополам вертикальной линией так, чтобы получились два прямоугольника.
В одном прямоугольнике нарисуйте линию, объединив противоположные углы.
Разверните эту линию горизонтально так, как это показано на рисунке.
Создайте еще один прямоугольник, используя горизонтальную линию, которую вы рисовали в предыдущих шагах как основу. Готово!
«Золотые» инструменты
Если чертить и вымерять не ваше любимое занятие, предоставьте всю «черную работу» инструментам, которые разработаны специально для этого. С помощью представленных ниже 4-х редакторов вы легко найдете Золотое сечение!
1. GoldenRATIO
Приложение GoldenRATIO помогает разрабатывать веб-сайты, интерфейсы и макеты в соответствии с Золотым Сечением.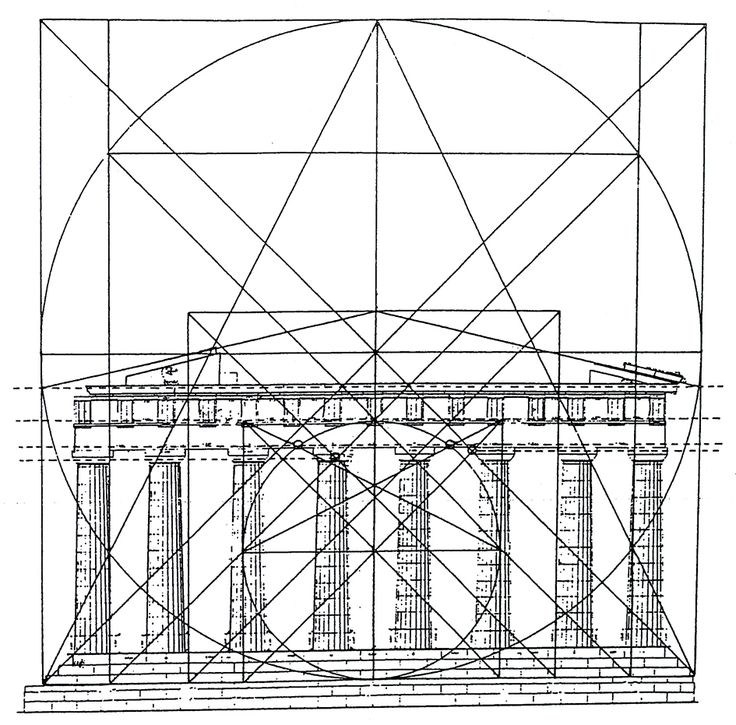 Оно доступно в Mac App Store за $ 2,99, и имеет встроенный калькулятор с визуальной обратной связью, и удобную функцию «Избранное», в которой хранятся настройки для повторяющихся задач. Совместимо с Adobe Photoshop.
Оно доступно в Mac App Store за $ 2,99, и имеет встроенный калькулятор с визуальной обратной связью, и удобную функцию «Избранное», в которой хранятся настройки для повторяющихся задач. Совместимо с Adobe Photoshop.
2. Golden Ratio Typography Calculator
Этот калькулятор, который поможет вам создать идеальную типографику для сайта в соответствии с принципами Золотой пропорции. Просто введите размер шрифта, ширину содержимого в поле на сайте, и нажмите «Set my type»!
3. Phicalculator
Это простое и бесплатное приложение для Mac и PC. Просто введите число, и он рассчитает для него пропорцию в соответствии с правилом Золотого сечения.
4. Atrise Golden Section
Удобная программа, которая избавит вас от необходимости расчетов и рисования сеток. С ней найти идеальные пропорции проще простого! Работает со всеми графическими редакторами, в том числе и Photoshop. Несмотря на то, что инструмент платный – 49$, есть возможность протестировать пробную версию в течение 30 дней.
kinolib.info
Золотое сечение
Золотое сечениеЗолотое сечение
Золотое сечение поистине уникальное число в математике! Встречается часто в природе, часто в соперничестве с наибольшее иррациональное число всех времен, p! Но в отличие от своего конкурента p, Золотое сечение — это конструируемое число! Официально золотое сечение обозначается символом Φ . По определению:
Ф 2 = Ф + 1
Φ -1 = Φ — 1 = φ
Введите любое положительное число:
| Золотое сечение Чтобы построить золотое сечение, все, что вам нужно сделать, это построить √5, добавить к нему 1 и разрезать его пополам. 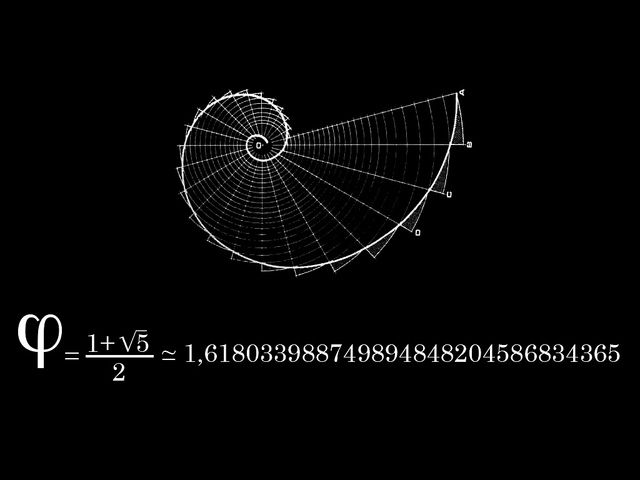
|
Еще один способ расчета золотого сечения — использование чисел Фибоначчи. Последовательность Фибоначчи имеет следующий вид:
f 1 = 1
f 2 = 1
f n = f n-2 + f n-1 , для n > 2.
Он имеет последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…, где следующий член является суммой двух предыдущих членов. Заметить, что
если вы делите последовательные термины, они приближаются к Φ.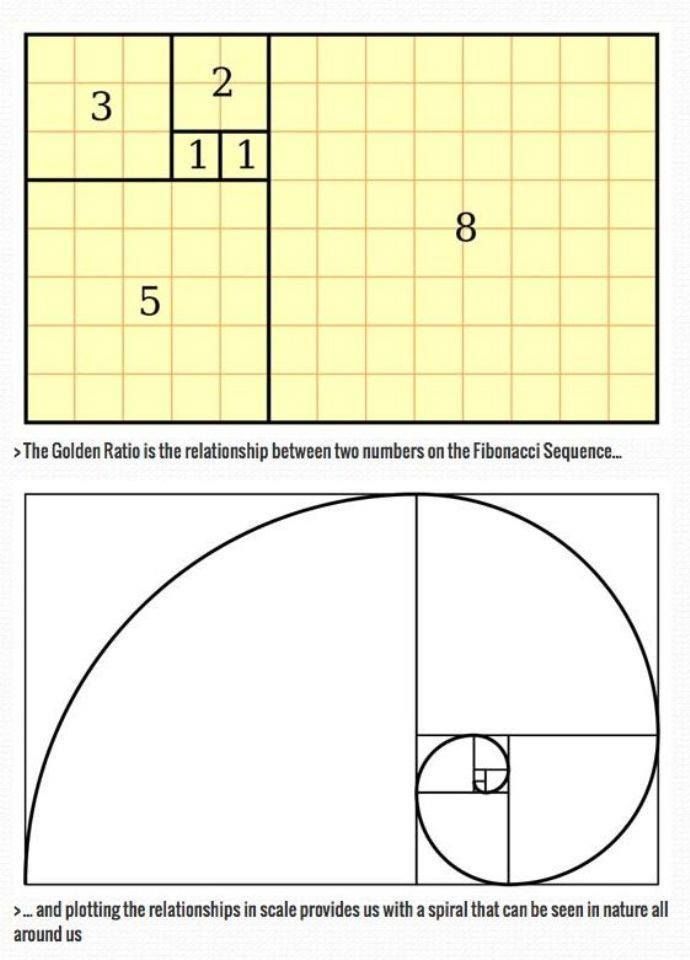 На самом деле он приближается довольно быстро, где 55/34 = 1,61764… .
На самом деле он приближается довольно быстро, где 55/34 = 1,61764… .
Золотой прямоугольник Золотой прямоугольник — это прямоугольник, у которого отношение длины к ширине равно Φ. Его относительно легко построить.
|
| Золотая спираль Золотая спираль создается путем построения золотых прямоугольников, вложенных друг в друга. Затем рисуется четверть дуги. по каждому квадрату. Золотую спираль также можно нарисовать с помощью равнобедренного треугольника 36° — 72° — 72°.  Золотой треугольник — это треугольник, находящийся внутри правильного пятиугольника. Золотой треугольник — это треугольник, находящийся внутри правильного пятиугольника. |
Полное руководство по его пониманию и использованию
Дизайнеры во всем мире должны знать о золотом сечении. Это математическое соотношение, которое создает эстетически привлекательный дизайн. Поскольку золотое сечение так часто встречается в природе, неудивительно, что его результаты выглядят естественно.
Фото Богомила Михайлова на Unsplash
Золотое сечение также имеет несколько других названий:
- Божественная пропорция
- Золотая середина
- Золотое сечение
- Фи (греческая буква)
- 1
Математика золотого сечения
- 1.1 Чтобы понять золотое сечение, вы должны сначала понять золотой прямоугольник.
- 1,2 Вернемся к Золотому прямоугольнику, потому что его намного легче понять.
- 1,3 Последовательность Фибоначчи
- 1,4 Золотые круги
- 2 Вы видели это раньше, много
- 3
Золотое сечение в искусстве и дизайне
- 3.
 1
Давайте взглянем на часто упоминаемый пример: Парфенон.
1
Давайте взглянем на часто упоминаемый пример: Парфенон.
- 3.
- 4
Золотое сечение и дизайн веб-сайта
- 4.1 Золотое сечение и макет
- 4.2 Золотое сечение и расстояние
- 4.3 Золотое сечение и содержание
- 4.4 Почетное упоминание: Золотое сечение и изображения
- 5 Подведение итогов
Математика золотого сечения
Я собираюсь объяснить математику золотого сечения как можно проще, не вдаваясь в детали, которые вам на самом деле знать не нужно. Если вы можете идти в ногу с математикой, отлично. Но если вы не можете, ничего страшного — вы все равно сможете использовать эту концепцию в своих проектах.
Чтобы понять золотое сечение, вы должны сначала понять золотой прямоугольник
Золотой прямоугольник — это большой прямоугольник, внутри которого находится квадрат. Стороны квадрата равны наименьшей длине прямоугольника:
Источник: Википедия
Золотое сечение — это число, которое (отчасти) равно 1,618, точно так же, как число Пи приблизительно равно 3,14, но не точно.
Вы берете линию и делите ее на две части – длинную часть (а) и короткую часть (б). Вся длина (a + b), деленная на (a), равна (a), деленная на (b). И оба эти числа равны 1,618. Итак, (a + b), деленное на (a), равно 1,618, а (a), деленное на (b) 9.0233 также равно 1,618.
Вернемся к Золотому прямоугольнику, потому что его намного легче понять
Когда вы помещаете квадрат внутрь прямоугольника, он создает другой, меньший прямоугольник. Не обращайте внимания на черные линии и посмотрите на красный и зеленый прямоугольники:
.Красный квадрат имеет четыре стороны одинаковой длины, и эта длина равна наименьшей длине прямоугольника. Разделив этот квадрат, вы автоматически создадите другой, меньший прямоугольник (обведен зеленым). Вместе они создают полный макет Золотого сечения и основу для Золотой спирали.
Вы также можете сделать новый золотой прямоугольник из меньшего прямоугольника, как этот, который я обвел синим цветом:
Традиционная диаграмма золотого сечения имеет восемь золотых прямоугольников:
А вот и самый маленький золотой прямоугольник, №8:
Если вы начнете в левом нижнем углу и сделаете арку, чтобы соединить дальнюю сторону каждого поперечного сечения квадрата и маленького прямоугольника, вы получите Золотую спираль.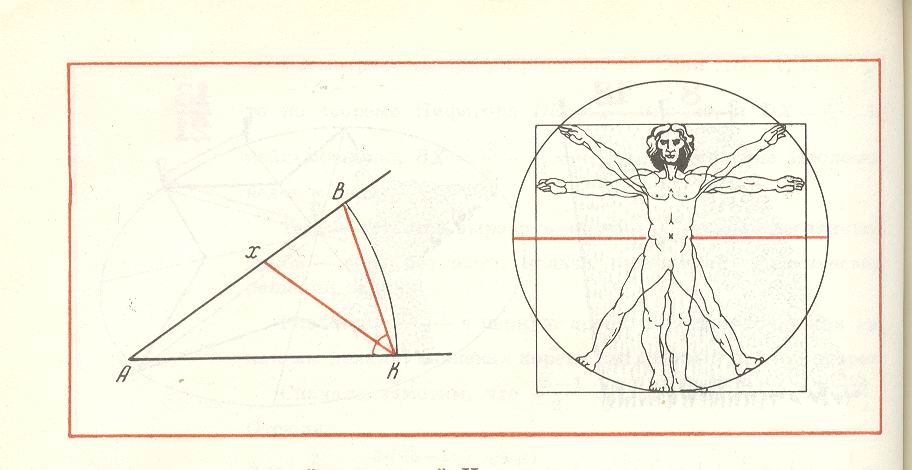
Последовательность Фибоначчи
Последовательность Фибоначчи довольно проста для понимания: вы начинаете с нуля и 1, затем получаете следующее число, складывая два числа перед ним. 0 + 1 = 1, затем 1 + 1 = 2 и т. д. Первые несколько чисел в последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
Если вы используете эти числа для создания квадратов такой ширины, вы можете создать Золотую спираль:
Источник: Math is Fun
Золотые круги
Иногда вместо спирали или в дополнение к ней на квадратах можно увидеть круги. Если вы нарисуете идеальные круги в ячейках наложения Золотого сечения, они будут иметь соотношение 1: 1,618 с одним соседним кругом.
Источник: Департамент Limelight
В логотипах Pepsi и Twitter используются золотые круги:
Источник: Hybrid Talks
Вы уже видели это раньше,
МногоПрирода полна золотого сечения. Это во флоре, ракушках, погоде…
Источник: Фото Энни Спратт на Unsplash
Источник: Фото НАСА на Unsplash
И поскольку мы видим его так часто, наш мозг предпочитает его. Эта врожденная привлекательность — вот почему это такой мощный макет для дизайнеров.
Эта врожденная привлекательность — вот почему это такой мощный макет для дизайнеров.
Золотое сечение в искусстве и дизайне
Иногда золотое сечение очень легко узнать:
Источник: staceysdetailinginc.com
Иногда вы говорите: «Я понятия не имею, о чем вы говорите… о, подождите. Теперь я это вижу. Я думаю.»
Источник: инсайдеры отдела маркетинга
В другое время можно было сойти с ума, глядя на это…
Источник: Широкие стены
…но если сосредоточиться на основном Золотом Прямоугольнике, то становится немного понятнее:
Давайте посмотрим на часто упоминаемый пример: Парфенон
Источник: Creative Bloq
Сначала вы можете увидеть это и сказать: «Мне это кажется симметричным. Как то, на что я смотрю, вписывается в эту золотую прямоугольную спираль?»
Золотое сечение не о том, как каждая часть дизайна вписывается полностью и только в определенные разделы. Если бы это было так, правая сторона Парфенона была бы одним большим блоком, а левая сторона была бы разделена на более мелкие блоки.
Вместо этого соотношение используется для создания гармонии и пропорции, и это можно интерпретировать несколькими способами.
Хотя золотое сечение основано на математике, его можно творчески адаптировать. В случае с Парфеноном золотое сечение определяет высоту и расположение компонентов дизайна. Кроме того, есть несколько способов наложить на него диаграммы золотого сечения:
Источник: Archinect
Источник: Эстер Сугихто на Medium
Источник: GoldenNumber.net
Золотое сечение и дизайн веб-сайта
Любите ли вы математику или ваша голова вот-вот взорвется, золотое сечение немного легче понять с точки зрения дизайна. Вы сделали тяжелую работу. Теперь пришло время взять базовое наложение и сделать ваши веб-компоненты идеально приятными.
Золотое сечение и макет
Если вам нужен идеальный макет с золотым сечением, установите размеры 1:1,618. Например, вы можете установить ширину 960 пикселей и высоту 59 пикселей. 4 пикселя. Золотой прямоугольник имеет 594 пикселя с каждой стороны, и прямоугольник занимает остальную часть макета (594 x 366).
4 пикселя. Золотой прямоугольник имеет 594 пикселя с каждой стороны, и прямоугольник занимает остальную часть макета (594 x 366).
Calculator Soup есть полезный калькулятор золотого сечения, в котором вы можете установить любой член (A, B или A + B), чтобы найти правильные значения золотого сечения.
Или вы можете просто использовать этот тип макета с двумя столбцами, где один столбец немного шире другого столбца. Он организован и четко показывает иерархию.
Источник: National Geographic
Я использую это на своем веб-сайте, потому что домашняя страница представляет собой набор сообщений в моем блоге, и я чувствую, что это один из самых узнаваемых макетов для блогов:
Однако, на мой взгляд, симметричный макет, который мы используем в Elegant Themes, более современный:
Золотое сечение и расстояние
Золотое сечение может помочь вам определить, где разместить элементы вашего дизайна, какие пропорции использовать и где оставить пустое пространство.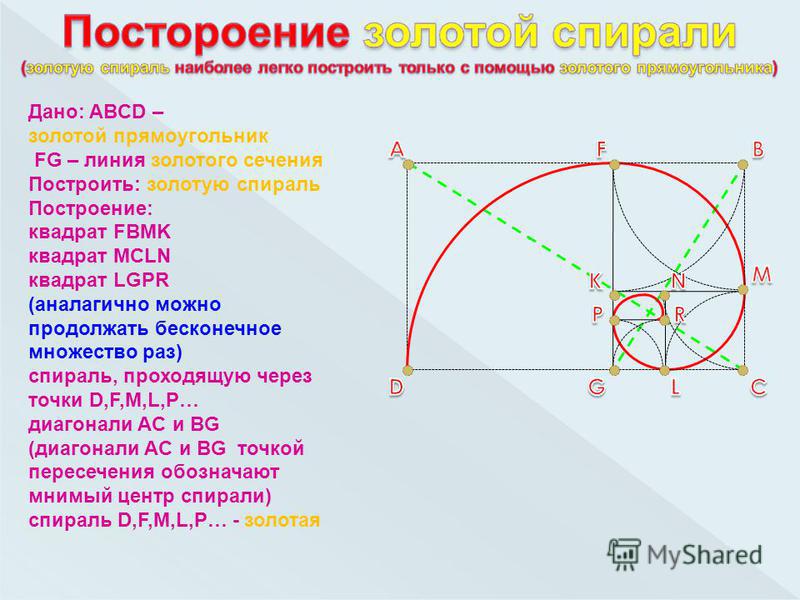 Вот простой пример, и вы можете почти увидеть наложение золотого сечения, даже не помещая его поверх:
Вот простой пример, и вы можете почти увидеть наложение золотого сечения, даже не помещая его поверх:
Источник: Digiarts 2011
Вот как это выглядит, когда я применяю Золотую спираль в Photoshop:
Опять же, золотое сечение основано на математике, но когда дело доходит до применения его в дизайне, оно не идеально. Этот дизайн не создан на основе Золотого прямоугольника, поэтому Золотая спираль имеет ненормальные пропорции. Тем не менее, вы можете видеть, как это может помочь дизайнеру выбрать, где разместить самый большой элемент дизайна, а также самые маленькие элементы и свободное пространство.
Вы также можете наложить наложение Golden Ratio, чтобы применить его к различным элементам одного и того же дизайна:
Источник: брендинг Lemongraphic. Пример из Канвы.
Золотое сечение и содержание
Когда вы думаете о макете Золотого сечения и интервалах вместе, вы можете начать решать, где размещать контент на своем веб-сайте.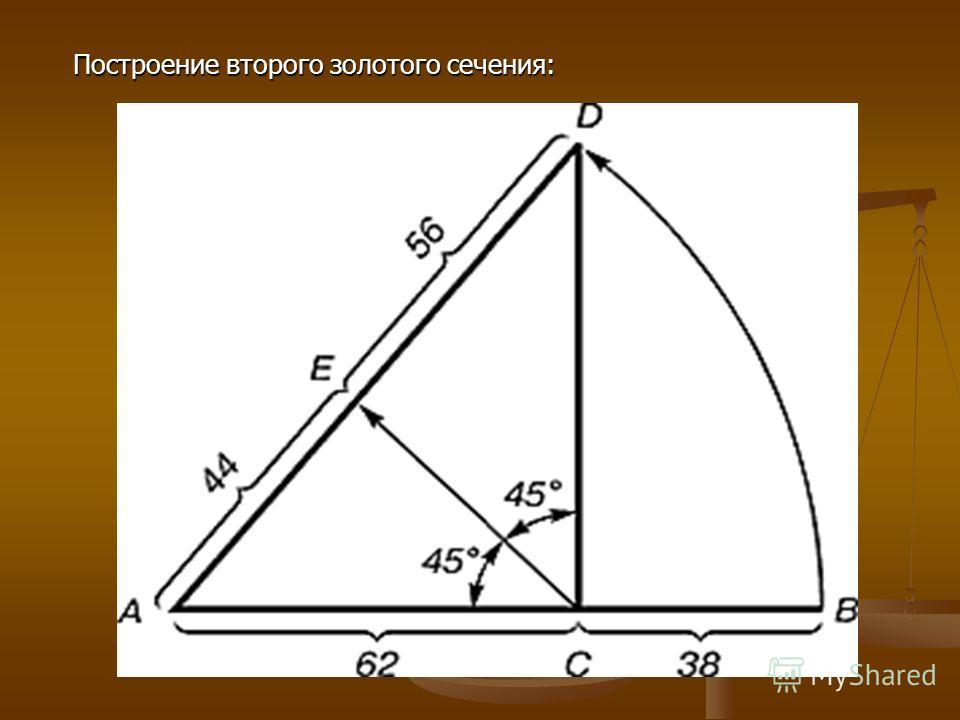
Давайте снова посмотрим на веб-сайт National Geographic, на этот раз с наложенным на него золотым сечением Canva:
Макет разделен таким образом, что содержимое выстраивается вдоль центральной линии спирали. Слева есть большой блок контента. Справа контент становится более плотным и появляется гораздо больше негативного пространства. Ближе к центральному завитку спирали вы увидите второй логотип National Geographic — нет лучшего способа продвигать домашний бренд, чем разместить его там, где обычно падает взгляд.
Вот отличный пример того, как Золотая спираль может провести ваш взгляд через дизайн, даже за его основной компонент. Это полезно, если у вас много контента, который нужно втиснуть на одну страницу. Вы также заметите, что даже с таким упакованным и детализированным дизайном там все еще есть свободное пространство.
Источник: Дизайн Helms Workshop. Пример из Канвы.
Почетное упоминание: Золотое сечение и изображения
Золотое сечение также используется в композиции фотографии. Вместо создания золотой спирали золотое сечение разбивает изображение на шесть блоков. В сетке этого типа используется то же золотое сечение: ширина и высота секций либо 1, либо 0,618.
Вместо создания золотой спирали золотое сечение разбивает изображение на шесть блоков. В сетке этого типа используется то же золотое сечение: ширина и высота секций либо 1, либо 0,618.
Источник: Canva
Затем вы используете пересечения для компоновки кадра. Цель — поместить предмет или основную часть предмета на одну из пересекающихся линий — предмет не должен располагаться по центру, а некоторые блоки должны быть оставлены пустыми (в большинстве случаев, как минимум — макросъемка и портреты крупным планом). заполнит почти весь кадр). Делая это, вы создаете более интересный портрет, чем если бы объект был в центре.
Гораздо более простой и доступный способ следовать этому правилу — использовать сетку «Правило третей», которая, вероятно, есть на встроенной камере вашего телефона или цифровой зеркальной фотокамере.
Вот фотография сына моей двоюродной сестры. Я наложил на него сетку правила третей, чтобы показать вам, где объект заполняет кадр, а где нет.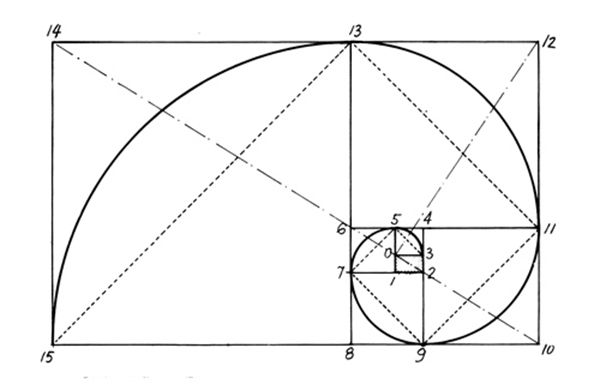
Также посмотрите, как Золотая спираль почти идеально обвивает объект:
Золотое сечение отличается от правила третей тем, что сетка правила третей имеет участки одинаковой длины и ширины. Однако это настолько близко — и намного проще — что это то, что фотографы обычно используют при составлении или редактировании фотографии.
Подведение итогов
Золотое сечение можно использовать как есть или адаптировать для ваших целей и настроить по размеру — в математике могут быть жесткие и быстрые правила, а в творчестве — нет. Хотя вы можете использовать золотое сечение с самого начала, чтобы направлять свой дизайн, вы также можете использовать его после того, как вы начали проектировать, чтобы вносить изменения и улучшения. Цель состоит в том, чтобы руководствоваться соотношением, а не насильно вписывать в него дизайн.
Готовы еще больше поиграть с макетом вашего веб-сайта? Ознакомьтесь с нашей статьей об использовании новых параметров высоты и ширины Divi для создания адаптивного дизайна.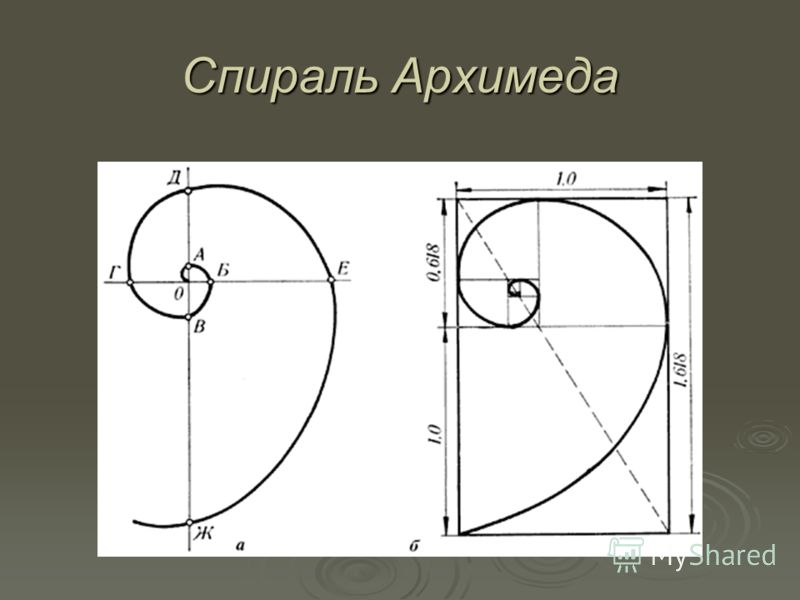

 1
Давайте взглянем на часто упоминаемый пример: Парфенон.
1
Давайте взглянем на часто упоминаемый пример: Парфенон.