Задачи на нахождение периметра и площади
Примеры решения задач разной сложности на нахождение периметра и площади
Условные обозначения и формулы
- a — длина
- b — ширина
- P — периметр
- S — площадь
Квадрат → определение
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Прямоугольник → определение
P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 – периметр прямоугольника
S = a · b — площадь прямоугольника
Задачи
Треугольник → определение
S = ½ · a · h – площадь треугольника
P = a + b + c – периметр треугольника
Задачи
Круг → определение
P = πD; P = 2πR — длина окружности
S = πR2; S = πD2 : 4 – площадь круга
Задачи
30 задач – от простого к сложному
Задача №1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)Ответ: периметр квадрата 32 см.
Задача №2
Найди периметр квадрата со стороной 16 см.
Решение:
16 · 4 = 64 (см)Ответ: периметр квадрата 64 см.
Задача №3
Периметр квадрата 16 см. Найди его сторону.
Решение:
16 : 4 = 4 (см)Ответ: сторона квадрата 4 см.
Задача №4
Найди периметр прямоугольника со сторонами 9 и 6 см.
Решение:
(9 + 6) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №5
Найди периметр прямоугольника со сторонами 7 и 8 см.
Решение:
(7 + 8) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №6
Найди длину прямоугольника, если его ширина 7 см, а периметр равен 40 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна ширина (сторона) 7 см, то и другая (противоположная) тоже 7 см.
7 + 7 = 14 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон (длин) будет равна:
40 — 14 = 26 (см)
Теперь узнаем длину одной стороны:
26 : 2 = 13 (см)
Ответ: длина прямоугольника 13 см. или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.

Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13Ответ: длина прямоугольника 13 см.
Задача №7
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Решение:
Вариант Ⅰ
10 + 10 = 20 (см)
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна длина (сторона) 10 см, то и другая (противоположная) тоже 10 см.
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон будет равна:
30 — 20 = 10 (см)
Теперь узнаем ширину одной стороны:
10 : 2 = 5 (см)Ответ: ширина прямоугольника 5 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = 10 см, b — ширина = ?, P — периметр = 30 см.
Составим уравнение:
(10 + b) · 2 = 30
20 + 2b = 30
2b = 30 — 20
2b = 10
b = 10 : 2
b = 5Ответ: ширина прямоугольника 5 см.
Задача №8
Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.
Решение:
14 + 5 = 19 (см)
(19 + 14) · 2 = 66 (см)
19 · 14 = 266 (см²)Ответ: периметр прямоугольника 66 см; площадь прямоугольника 266 см².
Задача №9
Длина прямоугольника 7 см. Ширина на 3 см меньше. Найди его периметр и площадь.
Решение:
7 — 3 = 4 (см)
(7 + 4) · 2 = 22 (см)
7 · 4 = 28 (см²)Ответ: периметр прямоугольника 22 см; площадь прямоугольника 28 см².
Задача №10
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)Ответ: площадь квадрата 36 см².
Задача №11
Периметр квадрата 36 см. Найди его площадь.
Решение:
36 : 4 = 9 (см)
9 · 9 = 81 (см²)Ответ: площадь квадрата 81 см².
Задача №12
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)Ответ: он ошибся на 3 см².
Задача №13
Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6.

На сколько см² он ошибся?Решение:
10 · 8 = 80 (см²)
8 · 6 = 48 (см²)
80 — 48 = 32 (см²)Ответ: он ошибся на 32 см².
Задача №14
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Решение:
4 + 4 = 8 (см)
36 — 8 = 28 (см)
28 : 2 = 14 (см)
14 · 4 = 56 (см²)Ответ: площадь прямоугольника 56 см².
Задача №15
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см)
3 + 3 = 6 (см)
24 — 6 = 18 (см)
18 : 2 = 9 (см)Ответ: длина прямоугольника 9 см.
Задача №16
Сторона квадрата 18 см.
Найди длину прямоугольника с таким же периметром и шириной 14 см.Решение:
18 · 4 = 72 (см)
14 + 14 = 28 (см)
72 — 28 = 44 (см)
44 : 2 = 22 (см)Ответ: длина прямоугольника 22 см.
Задача №17
Площадь прямоугольника 40 см². Ширина его 4 см.
Чему равен периметр прямоугольника?Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)Ответ: периметр прямоугольника 28 см.
Задача №18
Площадь прямоугольника 40 см². Длина его 8 см.
Чему равен периметр прямоугольника?Решение:
40 : 8 = 5 (см)
(8 + 5) · 2 = 26 (см)
Ответ: периметр прямоугольника 26 см.
Задача №19
Ширина прямоугольника 15 см, длина 20 см.

Найди длину другого прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.Решение:
в первом действии узнаём площадь по формуле a · b = S
15 · 20 = 300 (см²) — S одного и другого прямоугольника
теперь ширину второго
15 : 3 = 5 (см) — ширина другого прямоугольника
и отвечаем на вопрос задачи применив формулу S : a = b
300 : 5 = 60 (см)Ответ: длина другого прямоугольника 60 см.
Задача №20
Длина прямоугольника b = 32 см. Ширина a = 4 см.
Найди длину другого прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.Решение:
узнаем площадь прямоугольников по формуле a · b = S
32 · 4 = 128 (см²) — S первого прямоугольника
теперь ширину второго прямоугольника
4 · 2 = 8 (см) — ширина другого прямоугольника
применив формулу S : a = b узнаем длину другого
128 : 8 = 16 (см)Ответ: длина другого прямоугольника 16 см.
Задача №21
Какой участок земли потребует большую ограду: прямоугольный размерами 32 м и 2 м или квадратный, имеющий ту же площадь?
Решение:
Ⅰ. Прямоугольный участок
32 · 2 = 64 (м²) — S прямоугольного участка = 64 (м²)
(32 + 2) · 2 = 68 (см) — P прямоугольного участка = 68 (см)Ⅱ. Квадратный участок (имеющий площадь прямоугольного = 64 м²)
Если S квадрата = a · a, тогда, из формулы, узнаем сторону квадратного участка S : a = a
(у квадрата все стороны равны, тогда a · a = S — таблицу умножения мы знаем, подберём значения a и заменим их — 8 · 8 = S или 8 · 8 = 64 или 64 = 8 · 8 или 64 : 8 = 8)
64 : 8 = 8 (м) — любая сторона квадратного участка = 8 (м)
8 · 4 = 32 (м) — периметр квадратного участка = 32 (м)Ⅲ. P прям. — P квадр. = разница периметров
68 — 32 = 36 (м) — разница периметровОтвет: потребует большую ограду прямоугольный на 36 м.
Задача №22
Какая комната потребует больше плинтуса: прямоугольная размерами 4 м и 9 м или квадратная, имеющая ту же площадь?
Решение:
(4 + 9) · 2 = 26 (м) — P периметр прямоугольной комнаты
4 · 9 = 36 (м²) — S площадь прямоугольной комнаты
(из условия задачи квадратная комната имеет ту же площадь 36 м², а из определения площади квадрата знаем, что все стороны равны a = a = a = a, смотрим таблицу умножения и видим 6 · 6 = 36, то есть любая из сторон a = 6
запишем (приведём) формулу площади квадрата S = a · a в форму нахождения её стороны S : a = a
36 : 6 = 6 (м) — любая из сторон квадратной комнаты
6 · 4 = 24 (м) — P периметр квадратной комнаты
26 — 24 = 2 (м)Ответ: потребует больше плинтуса прямоугольная на 2 м.
Задача №23
Ребро куба равно 2 сантиметров.
Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)Ответ: площадь всех граней куба равна 24 см².
Задача №24
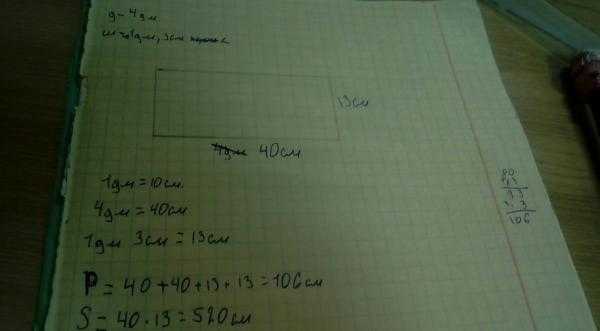
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение:
Для решения потребуются формулы:
S = a · a; S = a² — площадь квадрата (у квадрата все стороны равны)
S = a · b — площадь прямоугольника (у прямоугольника противоположные стороны равны)
Далее всё очень просто:Квадрат A.

S = a · a или a · a = S — формула площади квадрата, тогда
8 · 8 = 64 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 1 = 4 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь вырезанного прямоугольника
64 — 4 = 60Ответ: площадь получившейся фигуры равна 60.
Квадрат B.
S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 2 = 8 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 — 8 = 41Ответ: площадь получившейся фигуры равна 41.
Квадрат C.

S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
5 · 1 = 5 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 — 5 = 44Ответ: площадь получившейся фигуры равна 44.
Задача №25
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
(!) Фигуры расположены на листе в клетку, где каждая клетка – квадрат со стороной равной 1см.
Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу
Фигура A.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура B.

S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²Ответ: площадь фигуры B 20,5 см²
Фигура C.
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²Ответ: площадь фигуры C 30,5 см²
Фигура D.

S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры D
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура E.
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²Ответ: площадь фигуры E 12 см².
Задача №26
Найдите площади и периметры фигурок. Сделайте вывод.
Определение:
Периметр – сумма длин всех сторон фигуры выраженый в милиметрах, сантиметрах, дециметрах, метрах и т.д.Площадь фигуры – геометрическое понятие, размер плоской фигуры выраженый в мм², см², дм², м² и т.д.
Пусть каждая из сторон клетки равна 1 см, тогда
применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура A имеет четыре стороны, тогда
1 + 4 + 1 + 4 = 10 см — периметр фигуры.Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура B имеет четыре стороны, тогда
2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура C имеет шесть сторон, тогда
3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура D имеет восемь сторон, тогда
1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура E имеет восемь сторон, тогда
1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.Вывод:
Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат.
У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача №27
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + 8² = c²
6 · 6 + 8 · 8 = c²
36 + 64 = с²
с² = 36+64
с² = 100
с = 10
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №28
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (гипотенуза) с = 10 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + b² = 10²
6 · 6 + b² = 10 · 10
36 + b² = 100
b² = 100 — 36
с² = 64
с = 8
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №29
В треугольной пластине abc у которой один из углов 90°, сторона a равна 20 сантиметрам, а сторона b равна 10 сантиметрам просверлили отверстие диаметром 3 сантиметра. Какую оставшуюся площадь пластины нужно покрасить?
Решение:
Мы знаем что площадь – S треугольника равна половине – ½ произведения его основания – a умноженная на высоту – h, то есть S = ½ · a · h, а Формула площади круга S = πd² : 4, число π ≈ 3,14.
1) По условию задачи пластина имеет форму прямоугольника со сторонами abc, в данном случае сторона b является высотой треугольника.
Тогда формула будет выглядеть так – S = ½ · a · b
подставим значения в эту формулу
½ · 10 · 20 = 100 (см²) — площадь треугольника
2) Подставим значения в формулу и узнаем площадь круга S = πd² : 4
3,14 · 3² : 4 = 3,14 · 9 : 4 = 7,065 (см²)
3) Теперь мы можем ответить на вопрос поставленный в задаче
100 — 7,065 = 92,935 см² — оставшуюся площадь пластиныОтвет: нужно покрасить 92,935 см².
Задача №30
На садовом участке Петя построил для цыплят круглый вольер радиусом 5 метров. Участок имеет прямоугольную форму с длинной 120 метров и шириной равной 8 диаметрам вольера. Сколько потребуется метров металлической сетки чтобы огородить участок и вольер?
Решение:
Для решения задачи нам потребуются вычислить периметры участка и вольера.
1) В первом действии узнаем диаметр вольера, нам известен радиус 5 метров, тогда по формуле диаметр равен двум радиусам D = 2R
5 · 2 = 10 (м) — диаметр вольера
2) Если ширина участка равна 8 диаметрам вольера, тогда
10 · 8 = 80 м — ширина участка
3) Далее по формуле P = (a + b) · 2 — периметр прямоугольника
120 + 80 · 2 = 400 (м)
4) Теперь по формуле P = 2πR — длина окружности (периметр) вольера
2 · 3,14 · 5 = 2 · 3,14 · 5 = 31,4 (м)
5) В последнем действии сложим периметры участка и вольера ответим на вопрос задачи
400 + 31,4 = 431,4 (м)Ответ: потребуется 431,4 метров металлической сетки.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Рене Декарт
математик, философ
Дата рождения: 31 марта 1596 г.
Место рождения: Декарт, Турень, Абсолютная монархия во Франции
Дата смерти: 11 февраля 1650 г. (53 года), Стокгольм, Швеция
Биография
Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (ныне Декарт), департамент Эндр и Луара, Франция. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Начальное образование Декарт получил в иезуитском колле́же Ла Флеш, где его учителем был Жан Франсуа.
В коллеже Декарт познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции, и Жаком Валле де Барро. Религиозное образование только укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционной Голландии (в те годы — союзнице Франции), затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война).
В Голландии в 1618 году Декарт познакомился с выдающимся физиком и натурфилософом Исааком Бекманом, оказавшим значительное влияние на его формирование как учёного. Несколько лет Декарт провёл в Париже, предаваясь научной работе, где, помимо прочего, открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.
Затем — ещё несколько лет участия в войне (осада Ла-Рошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
В 1634 году он заканчивает свою первую, программную книгу под названием «Мир» (Le Monde), состоящую из двух частей: «Трактат о свете» и «Трактат о человеке». Вскоре, однако, одна за другой, появляются другие книги Декарта.
Кардинал Ришельё благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции. Протестантские же богословы Голландии наложили на них проклятие (1642)
В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины (с которой много лет активно переписывался) и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер.
Его труды:
- Сформулировал (хотя и не доказал) основную теорему алгебры
- Методы решения алгебраических уравнений
- Классификация алгебраических кривых
- Сформулировал точное «правило знаков» для определения числа положительных корней уравнения
- Исследовал алгебраические функции (многочлены)
- Исследования Декарта в области к механики, оптики и общему строению Вселенной
- Математически вывел закон преломления света
- Понятие о рефлексе
- Классическое построение философии рационализма
- Теория близкодействия
- Метод радикального сомнения
- Картезианский дуализм
В память о Декарте:
- Великий физиолог И.
 П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
П. Павлов поставил памятник-бюст Декарту возле своей лаборатории - В честь учёного названы его родной город
- Назван кратер на Луне
- Назван астероид (3587) Descartes
- Декартова система координат
- Декартов лист
- Декартов овал
- Декартово дерево
- Декартово произведение
***
Цитата: У одного человека зачастую больше шансов сделать открытие, нежели у нескольких, занимающихся одной проблемой.
Выбираем мебель | Советы по выбору мебели от Столплит
Вы точно хотите удалить выбранный товар? Отменить действие будет невозможно
Как ухаживать за диванами?
Дата публикации: 13.04.2021
Для того, чтобы ваш любимый диванчик служил вам долго и радовал глаз, нужно просто соблюдать некоторые правила ухода за тканью, из которого он сделан.

В данной статье рассмотрим варианты ухода за различными тканями.
Как правильно выбрать матрас?
Дата публикации: 17.07.2020
Современные технологии и материалы позволяют производить матрасы, которые стали не просто предметом обязательного использования на кровати, но и средством избавления от разных проблем со здоровьем. Благодаря своим характеристикам матрас способствует здоровому и качественному сну, а значит отличному утреннему настроению.
Правильная расстановка мебели в однокомнатной квартире
Дата публикации: 06.10.
 2019
2019Даже в однокомнатной квартире небольшой площади есть место для полета фантазии, возможность в полной мере раскрыть талант дизайнера.
Для проведения важного мероприятия, такого как расстановка мебели, однокомнатная квартира имеет слишком ограниченное пространство, которое нужно заполнять только действительно нужными вещами.
Проблему ограниченности пространства способно решить приобретение удобной и функциональной мебели, рациональное использование каждого квадратного сантиметра площади, четкое представление владельца о том, с какой целью планируется использовать каждый конкретный уголок.
Оптимальная расстановка мебели в прихожей
Дата публикации: 06.10.2019
Зачастую такому помещению, как прихожая, отводится слишком малая площадь либо очень неудобная форма, благодаря чему расстановка мебели в прихожей — задача сложная, но вполне выполнимая
Внешний вид прихожей может многое сказать пришедшим впервые гостям об образе жизни и роде занятий хозяина, его увлечениях и характере.
 Поэтому к созданию интерьера прихожей и расстановке мебели в ней стоит подойти максимально ответственно и внимательно.
Поэтому к созданию интерьера прихожей и расстановке мебели в ней стоит подойти максимально ответственно и внимательно.Правильная расстановка мебели в детской комнате
Дата публикации: 06.10.2019
Одним из важнейших требований, предъявляющихся к планировке и оформлению дизайна комнаты для детей — это практичность. Расстановка мебели в детской комнате предполагает создание в ней особой атмосферы уюта и удобства.
В детской комнате каждый квадратный сантиметр необходимо использовать с максимальной пользой. Каждый элемент интерьера и предмет мебели необходимо гармонично увязывать как друг с другом, так и со всей концепцией, комната должна быть выдержана в едином стиле. Потому необходим тщательный выбор обстановки, цвета мебели, ее фактуры.
org/Article»>Грамотная расстановка мебели в спальне
Дата публикации: 06.10.2019
Само предназначение спальни требует особого отношения и внимательного подхода к планировке и расстановке мебели в этой комнате.
 Расстановка мебели в спальне должна осуществляться таким образом, чтобы обеспечить атмосферу спокойствия и комфорта, благоприятствующую ночному отдыху.
Расстановка мебели в спальне должна осуществляться таким образом, чтобы обеспечить атмосферу спокойствия и комфорта, благоприятствующую ночному отдыху.Задача по расстановке мебели значительно облегчается, если спальня имеет большую площадь, и имеет правильную форму, позволяющую расположить мебель в соответствии с правилами эргономики. В случае если комната имеет неправильную форму, а площадь ее ограничена до такой степени, что в ней можно разместить только самую необходимую мебель, расстановка мебели потребует приложения немалых сил и фантазии.
Правильная расстановка мебели в гостиной
Дата публикации: 06.10.2019
Гостиная считается именно той комнатой, в которой хозяева квартиры проводят большую часть своего времени, отдыхая или принимая гостей, общаясь с друзьями.
 Расстановка мебели в гостиной позволяет создать уют и комфортные условия для релаксации.
Расстановка мебели в гостиной позволяет создать уют и комфортные условия для релаксации.Для облегчения и упрощения расстановки необходимо сначала вычертить план комнаты на листе бумаги и в масштабе расположить все необходимые предметы мебели. Также на сайте нашей компании имеется специальная программа для расстановки мебели в гостиной, позволяющая в трехмерном пространстве с легкостью подобрать всю необходимую мебель и расположить ее согласно своим желаниям и предпочтениям.
Расстановка мебели на кухне: нюансы и способы
Дата публикации: 06.10.2019
Какой бы формы и размера ни была кухня, расстановка мебели в ней должна быть максимально удобной, практичной и в то же время красивой. Для этих целей разработана специальная трехмерная программа расстановки кухонной мебели, воспользоваться которой можно в соответствующем разделе сайта нашей компании.

Но лучше всего проявить фантазию и попробовать расставить мебель самостоятельно, попробовав различные варианты расстановки мебели на кухне.
Основные правила расстановки мебели
Дата публикации: 05.10.2019
Сделать интерьер любой комнаты уютным можно при помощи правильной и сбалансированной расстановки мебели. Предметы мебели необходимо выбирать не только исходя из их необходимости, но и учитывать назначение помещения, стиль в котором его планируется оформить. Зачастую обычной перестановкой мебели можно изменить комнату до неузнаваемости — никаких препятствий для полета фантазии нет.
Расстановка мебели в двухкомнатной квартире
Дата публикации: 05.
 10.2019
10.2019Интерьер и расстановка мебели в двухкомнатной квартире в первую очередь зависят от количества проживающих в ней людей, их возрастной и половой принадлежности. Несмотря на влияющие на расстановку факторы, все же имеются общие принципы назначения функциональных ролей комнатам. В любом случае какая-либо из комнат будет исполнять роль гостиной, другая комната, соответственно, станет спальней либо детской. И только прихожей сложно отвести какую-то другую роль.
Как расставить мебель в комнате с нишей?
Дата публикации: 05.10.2019
Ниша дает простор полету фантазии, в таких комнатах можно предусмотреть для ниш различное функциональное применение. Если в квартире имеется комната с нишей, расстановка мебели в ней должна осуществляться в зависимости от того, для каких целей предназначена сама комната — спальня, гостиная или детская.
 ..
..Расстановка мебели на даче
Дата публикации: 05.10.2019
Основное предназначение дачного домика — это отдохнуть на свежем воздухе и соприкоснуться с природой. Дачные дома сейчас в большинстве своем — это отнюдь не одноэтажные старенькие постройки, а полноценные жилые дома с подведенными коммуникациями. Расстановка мебели на даче — достаточно специфическая задача, не имеющая стандартных решений для всех случаев, требующая приложения фантазии и учета множества факторов.
Расстановка мебели в маленькой комнате
Дата публикации: 05.10.2019
К сожалению, далеко не все семьи могут позволить себе приобретение просторных квартир, в которых комнаты имеют достаточную площадь.
 Расстановка мебели в маленькой комнате считается задачей весьма непростой, ведь в этом случае необходимо разместить в ограниченном пространстве все требующиеся предметы, а от установки некоторых придется и вовсе отказаться.
Расстановка мебели в маленькой комнате считается задачей весьма непростой, ведь в этом случае необходимо разместить в ограниченном пространстве все требующиеся предметы, а от установки некоторых придется и вовсе отказаться.Расстановка мебели в трехкомнатной квартире — нюансы и особенности
Дата публикации: 02.10.2019
Трехкомнатная квартира — прекрасный полигон для экспериментов при оформлении интерьера. Расстановка мебели в трехкомнатной квартире не относится к слишком сложным процессам, в отличие от однокомнатных квартир, в которых одна комната должна выполнять функции сразу нескольких помещений. Однако, и здесь имеются свои особенности.
Расстановка мебели в хрущевке
Дата публикации: 02.
 10.2019
10.2019Много лет назад для устранения проблемы с нехваткой жилья для советских граждан ударными темпами велось строительство хрущевок, при этом главными задачами являлось максимально быстрое возведение домов при минимизации затрат, а не удобная планировка и комфорт проживания.
Несмотря на то, что в большинстве случаев в таких домах не соблюдаются современные нормы планировки для жилых помещений, правильная расстановка мебели в хрущевке сможет скрыть огрехи проектирования и поможет создать уют и комфорт.
Расстановка мебели в прямоугольной комнате — нюансы
Дата публикации: 02.10.2019
Чаще всего комнаты в наших квартирах имеют прямоугольную форму, о чем нередко сожалеют дизайнеры не особо жалующие прямоугольные помещения.
 Свидетельством этому может служить тот факт, что прямоугольная комната расстановка мебели фото редко можно увидеть на сайтах агентств и в портфолио дизайнеров.
Свидетельством этому может служить тот факт, что прямоугольная комната расстановка мебели фото редко можно увидеть на сайтах агентств и в портфолио дизайнеров.Оптимальная расстановка мебели в квадратной комнате
Дата публикации: 02.10.2019
При расстановке мебели в комнате, имеющей одинаковую длину и ширину, необходимо проявление фантазии и смекалки. Несмотря на то, что существуют определенные рекомендации, при расстановке мебели в квадратных комнатах необходимо отталкиваться от собственных вкусов и предпочтений, площади комнаты и требующейся мебели для комфортного проживания.
Где купить угловой диван
Дата публикации: 25.
 06.2019
06.2019Угловой диван – актуальный пример удобной и стильной мебели для вашей гостиной. Чтобы не сомневаться, где купить угловой диван, отправляйтесь в фирменные мебельные салоны или интернет-магазины, реализующие сертифицированные изделия от производителя.
Как выбрать письменный стол
Дата публикации: 27.05.2019
Письменный стол незаменим в интерьере кабинета или детской комнаты. Чтобы работать за ним было комфортно, необходимо учесть несколько ключевых моментов. Как выбрать письменный стол, узнайте прямо сейчас.
Оптимальная расстановка мебели в офисе
Дата публикации: 06.10.2019
Расстановка мебели в офисе является не такой уж и простой задачей, как может показаться на первый взгляд. Мало просто приобрести и разместить мебель, нужно сделать это таки образом, чтобы обеспечить максимальное удобство для работающих людей, сделать их труд эффективным и качественным. При расстановке мебели в таких специфических помещениях, как офисы, необходимо обладание специфическими знаниями, понимание правил и норм размещения сотрудников, некоторая хитрость.
Страницы: ◂Предыдущая 1 2 3 … 9 10 Следующая▸
Четырехугольники. Свойства прямоугольника, квадрата, параллелограмма, ромба, трапеции
8 минут чтения
В евклидовой геометрии четырехугольник — это четырехсторонняя двумерная фигура, сумма внутренних углов которой равна 360°. Слово «четырехугольник» происходит от двух латинских слов «quadri» и «latus», что означает «четыре» и «сторона» соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольников? Четырехугольники обладают двумя свойствами:
Слово «четырехугольник» происходит от двух латинских слов «quadri» и «latus», что означает «четыре» и «сторона» соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольников? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4 сторонами
- Сумма всех внутренних углов четырехугольника до 360°
В этой статье вы получите представление о 5 типах четырехугольников (Прямоугольник, Квадрат, Параллелограмм , ромб и трапеция) и узнать о свойствах четырехугольников.
Вот пять типов четырехугольников, обсуждаемых в этой статье:
- Прямоугольник
- Квадрат
- Параллелограмм
- Rhombus
- Trapezium
Вот видео, объясняющее свойства четырехугольника:
Это то, что вы прочитаете в статье:
[Hide]
.
 На приведенной ниже схеме изображен четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов равна 360°. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°
На приведенной ниже схеме изображен четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов равна 360°. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°| Свойства четырехугольников | Rectangle | Square | Parallelogram | Rhombus | Trapezium | ||||||||
| All Sides are equal | No | Yes | No | Yes | No | ||||||||
| Противоположные стороны равны | Да | Да | Да | Да | Нет | ||||||||
| Противоположные стороны параллельны | Yes | Yes | Yes | Yes | Yes | ||||||||
| All angles are equal | Yes | Yes | No | No | No | ||||||||
| Opposite angles are equal | Yes | Да, | Да, | Да, | № | ||||||||
| Сумма двух соседних углов — 180 | Да | Да | Да | Да | Но. | Да | Да | Но. | Но Но Но Но Но Но НоДа | Да | Но | Да | Да0067 |
| Bisect each other | Yes | Yes | Yes | Yes | No | ||||||||
| Bisect perpendicularly | No | Yes | No | Yes | No |
Let’s discuss each из этих 5 четырехугольников в деталях:
Вот вопросы, которые научат вас, как применять свойства всех 5 четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник – это четырехугольник с четырьмя прямыми углами. Таким образом, все углы прямоугольника равны (360°/4 = 90°). Более того, противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Вот три свойства прямоугольника:
- Все углы прямоугольника равны 90°
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника – площадь и периметр прямоугольника
Если длина прямоугольника равна L, а ширина равна B, то
- Площадь прямоугольника = длина × ширина или L × B
- Периметр прямоугольника = 2 × (L + B)
Эта практика вопросы помогут вам укрепить свойства прямоугольников
Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса, то есть сдать GMAT.
Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.
Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.
Квадрат
Квадрат – это четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, поскольку обе его стороны и углы равны. Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Вот три свойства квадрата:
- Все углы квадрата равны 90°
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга перпендикулярно
Формула квадрата – площадь и периметр квадрата
Если сторона квадрата равна а, то
- Площадь квадрата = а × а = а²
- Периметр квадрата = 2 × (а + а) = 4а
Эти практические вопросы помогут вам закрепить свойства квадратов. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:
youtube.com/embed/Hx5TgTucO8U?rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, он имеет две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а их диагонали делят друг друга пополам.
Вот четыре свойства параллелограмма:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов равна 180°
Формулы параллелограмма – площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина равна «b», а высота равна «h», то:
- Периметр параллелограмма = 2 × (l + б)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма параллельно друг другу.
Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
Вот четыре свойства ромба:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов равна 180 °
Формулы ромба – площадь и периметр ромба
Если сторона ромба равна а, то периметр ромба = 4а
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (называемая в США трапецией) — это четырехугольник, у которого только одна пара параллельных сторон. Параллельные стороны называются «основаниями», а две другие стороны называются «ногами» или боковыми сторонами.
Трапецией называется четырехугольник, у которого выполняется одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции – площадь и периметр трапеции
Если высота трапеции равна ‘ h’ (как показано на диаграмме выше), тогда:
- Периметр трапеции = сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции. и периметр различных типов четырехугольников:
Формулы четырехугольника Прямоугольник Square Parallelogram Rhombus Trapezium Area l × b a² l × h ½ × d1 × d2 ½ × (сумма параллельных сторон) × высота Периметр 2 × (L + B) 4A 2 × (L + B) 4A SOM SOME SIPE0067 Дополнительная литература:
- Формулы окружности – площадь и периметр
- Свойства чисел – четные и нечетные | Прайм | HCF & LCM
- Свойства треугольников – Определение | Типы | Классификация
- Линии и углы.
Свойства и их применение
Чтобы успешно сдать GMAT, требуется четко определенный учебный план. Сэкономьте 60+ часов на подготовке к GMAT, выполнив следующие три шага:
Четырехсторонний практический вопрос
Давайте попрактикуемся в применении свойств четырехугольников, ответив на следующие примеры вопросов:
GMAT: Практический вопрос четырехугольников 1
Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров. Сколько метров забора он должен купить, чтобы огородить весь сад?
- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
Шаг 1: Дано
- У Адама прямоугольный сад.
- Имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: Найти
- Длина, необходимая для возведения забора вокруг всего сада.
Этап 3: Подход и разработка
Забор можно построить только вокруг внешних сторон сада.
- Итак, общая длина необходимого забора = сумма длин всех сторон сада.
- Поскольку сад прямоугольный, сумма длин всех сторон есть не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Отсюда необходимая длина забора 50 метров.
Таким образом, вариант Е является правильным ответом.
GMAT: практика четырехугольников, вопрос 2
Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стен составляет 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Решение
Шаг 1: дано
- Стев хочет нарисовать одну стену из его комнаты.
- Длина стены 25 метров, ширина 18 метров.
- Стоимость покраски стены $1,5 за квадратный метр.
Шаг 2: Найти
- Общая стоимость покраски стены.
Этап 3: Подход и разработка
- Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы получим общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 долл. США = 675 долл. США
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти понятия для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.
Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.
Вот еще несколько статей по математике:
- Повышение точности математических вопросов о полигонах
- Вопросы по геометрии – самые распространенные ошибки | GMAT Quant Prep
Посмотрите этот вебинар без геометрии GMAT, на котором мы обсуждаем, как решать 700-уровневые вопросы достаточности данных и проблемные вопросы в GMAT Quadrilaterals:
Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса, то есть сдать GMAT. Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии.
Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.
Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.
Часто задаваемые вопросы
Какие существуют типы четырехугольников?
Существует 5 типов четырехугольников – прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.
Где я могу найти несколько практических вопросов по четырехугольникам?
В этой статье вы можете найти несколько практических вопросов по четырехугольникам.
Чему равна сумма внутренних углов четырехугольника?
Сумма внутренних углов четырехугольника равна 360°.
Площадь и периметр прямоугольника
Горячая математикаПрямоугольник – это параллелограмм с четырьмя прямыми углами.
Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.
периметр п прямоугольника находится по формуле п «=» 2 л + 2 ж , где л это длина и ж это ширина прямоугольника.
область А прямоугольника находится по формуле А «=» л ж , где л это длина и ж это ширина.
Вы часто будете сталкиваться с текстовыми задачами, когда заданы два значения в одной из этих формул, а вам нужно найти третье.
Пример 1:
Периметр прямоугольного бассейна равен 56 метров. Если длина бассейна 16 метров, затем найдите его ширину.
Здесь заданы периметр и длина прямоугольного бассейна. Нам нужно найти ширину бассейна.
Периметр п прямоугольника находится по формуле п «=» 2 л + 2 ж , где л это длина и ж это ширина прямоугольника.
Учитывая, что периметр 56 метров, а длина 16 метров. Итак, подставляем эти значения в формулу.
56 «=» 2 ( 16 ) + 2 ж
Упрощать.
56 «=» 32 + 2 ж
Вычесть 32 с обеих сторон.
24 «=» 2 ж
Разделите каждую сторону на 2 .
12 «=» ж
Следовательно, ширина прямоугольного бассейна равна 12 метров.
Пример 2:
Площадь прямоугольного забора равна 500 квадратный фут. Если ширина забора 20 футов, затем найдите его длину.
Здесь даны площадь и ширина прямоугольного забора. Нам нужно найти длину забора.
Площадь А прямоугольника находится по формуле А «=» л ж , где л это длина и ж это ширина.
Учитывая, что площадь 500 квадратных метров, а ширина 20 ноги. Итак, подставляем эти значения в формулу.
500 «=» л × 20
Разделите каждую сторону на 20 изолировать л .
25 «=» л
Следовательно, длина прямоугольного забора равна 25 ноги.










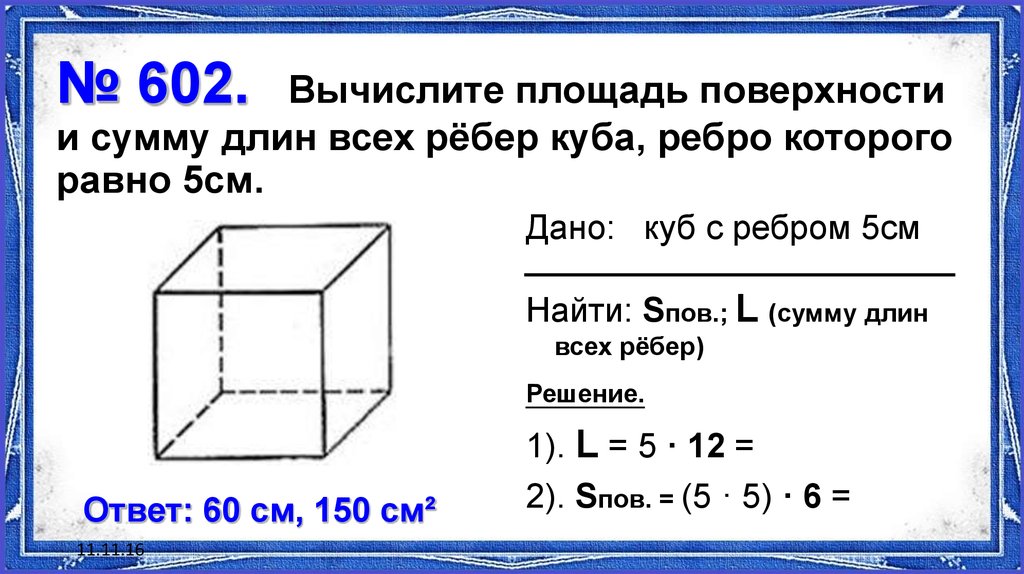
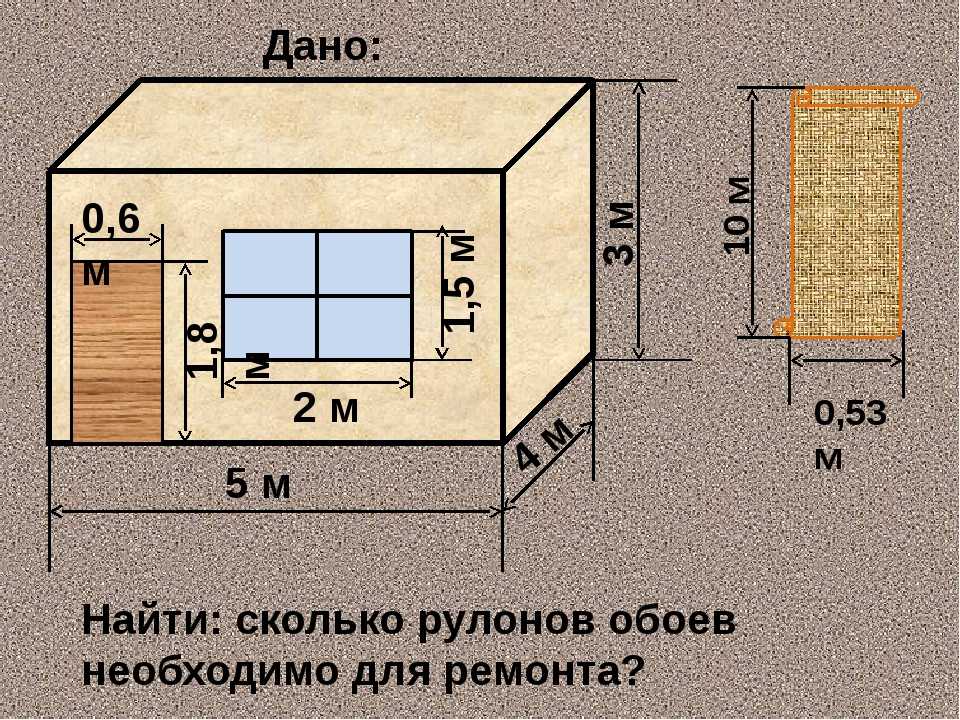
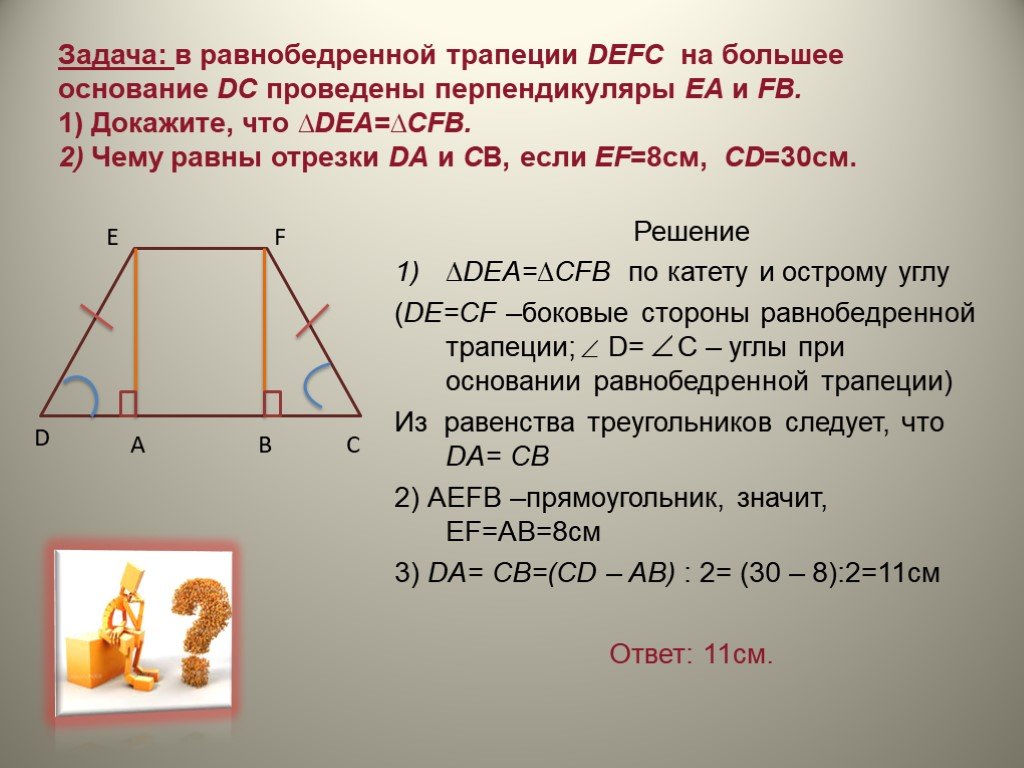 Найти площадь всех граней куба.
Найти площадь всех граней куба.







 П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
 2019
2019 Поэтому к созданию интерьера прихожей и расстановке мебели в ней стоит подойти максимально ответственно и внимательно.
Поэтому к созданию интерьера прихожей и расстановке мебели в ней стоит подойти максимально ответственно и внимательно. Расстановка мебели в спальне должна осуществляться таким образом, чтобы обеспечить атмосферу спокойствия и комфорта, благоприятствующую ночному отдыху.
Расстановка мебели в спальне должна осуществляться таким образом, чтобы обеспечить атмосферу спокойствия и комфорта, благоприятствующую ночному отдыху. Расстановка мебели в гостиной позволяет создать уют и комфортные условия для релаксации.
Расстановка мебели в гостиной позволяет создать уют и комфортные условия для релаксации.
 10.2019
10.2019 ..
.. Расстановка мебели в маленькой комнате считается задачей весьма непростой, ведь в этом случае необходимо разместить в ограниченном пространстве все требующиеся предметы, а от установки некоторых придется и вовсе отказаться.
Расстановка мебели в маленькой комнате считается задачей весьма непростой, ведь в этом случае необходимо разместить в ограниченном пространстве все требующиеся предметы, а от установки некоторых придется и вовсе отказаться. 10.2019
10.2019 Свидетельством этому может служить тот факт, что прямоугольная комната расстановка мебели фото редко можно увидеть на сайтах агентств и в портфолио дизайнеров.
Свидетельством этому может служить тот факт, что прямоугольная комната расстановка мебели фото редко можно увидеть на сайтах агентств и в портфолио дизайнеров.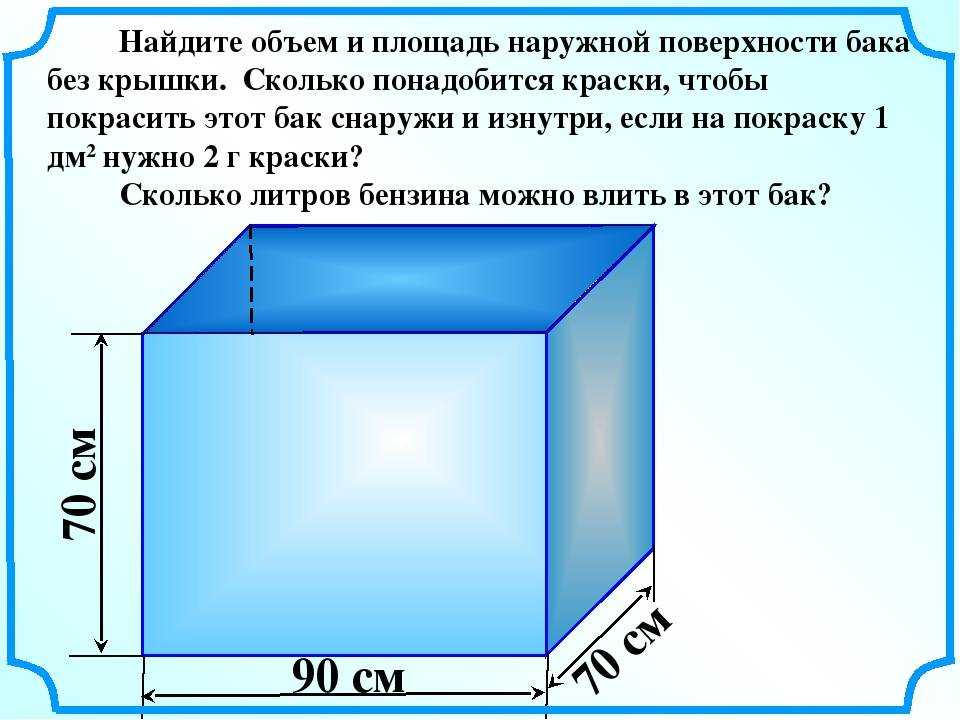 06.2019
06.2019 Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.
Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года. Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
 Свойства и их применение
Свойства и их применение

 Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.
Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.
Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.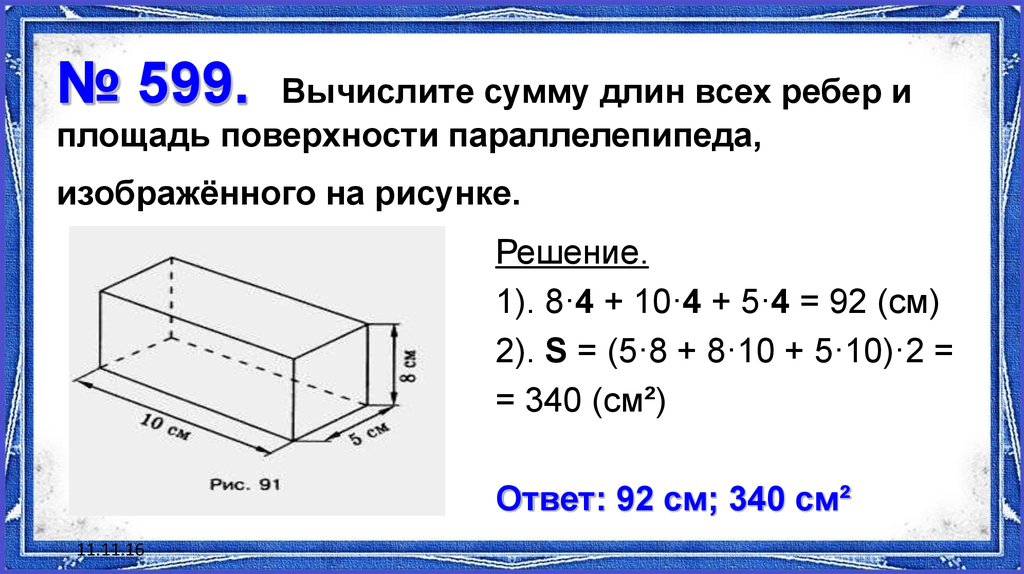 Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Все прямоугольники также являются параллелограммами, но не все параллелограммы являются прямоугольниками.

