Руководство по эксплуатации: Золотое сечение
Золотое сечение – это простой принцип, который поможет сделать дизайн приятным для визуального восприятия. В этой статье мы подробно расскажем как и зачем его использовать.
Распространенная в природе математическая пропорция, называемая Золотое сечение, или Золотая середина, основана на Последовательности Фибоначчи (о которой вы, скорее всего, слышали в школе, или читали в книге Дэна Брауна «Код да Винчи»), и подразумевает под собой соотношение сторон 1:1,61.
Такое соотношение сплошь и рядом встречается в нашей жизни (ракушки, ананасы, цветы и т.д.) и поэтому воспринимается человеком как нечто естественное, приятное взгляду.
→ Золотое сечение это взаимосвязь между двумя числами в последовательности Фибоначчи → Построение этой последовательности в масштабе дает спирали, которые можно увидеть в природе.Считается, что Золотое сечение используется человечеством в искусстве и дизайне уже более 4 тысяч лет, а возможно даже больше, если верить ученым, которые утверждают, что древние Египтяне использовали этот принцип при строительстве пирамид.
Знаменитые примеры
Как мы уже говорили, Золотое сечение можно видеть на протяжении всей истории искусства и архитектуры. Вот некоторые примеры, которые только подтверждают обоснованность использования этого принципа:
Архитектура: Парфенон
В древнегреческой архитектуре Золотое сечение использовалось для вычисления идеальной пропорции между высотой и шириной здания, размеров портика, и даже расстояния между колоннами. В дальнейшем, этот принцип был унаследован архитектурой неоклассицизма.
Искусство: Тайная вечеря
Для художников композиция – основа основ. Леонардо да Винчи, как и многие другие художники, руководствовался принципом Золотого сечения: в Тайной Вечере, к примеру, фигуры учеников расположены в нижних двух третях (большее из двух частей Золотого сечения), а Иисус помещен строго по центру между двумя прямоугольниками.
Веб-дизайн: редизайн Twitter в 2010
Креативный директор Twitter Дуг Боуман (Doug Bowman) опубликовал скриншот в своем аккаунте Flickr, объясняя использование принципа Золотого сечения для редизайна 2010 года. «Все, кто интересуется #NewTwitter пропорциями – знайте, все сделано не просто так», сказал он.
«Все, кто интересуется #NewTwitter пропорциями – знайте, все сделано не просто так», сказал он.
Apple iCloud
Иконка сервиса iCloud тоже совсем не случайный набросок. Как объяснил Такамаса Мацумото в своем блоге (оригинальная японская версия здесь) все построено на математике Золотого сечения, анатомию которого можно увидеть на рисунке справа.
Как построить Золотое сечение?
Нарисуйте квадрат. Это сформирует длину “короткой стороны” прямоугольника.
Разделите квадрат пополам вертикальной линией так, чтобы получились два прямоугольника.
В одном прямоугольнике нарисуйте линию, объединив противоположные углы.
Разверните эту линию горизонтально так, как это показано на рисунке.
Создайте еще один прямоугольник, используя горизонтальную линию, которую вы рисовали в предыдущих шагах как основу. Готово!
Готово!
«Золотые» инструменты
Если чертить и вымерять не ваше любимое занятие, предоставьте всю «черную работу» инструментам, которые разработаны специально для этого. С помощью представленных ниже 4-х редакторов вы легко найдете Золотое сечение!
1. GoldenRATIO
Приложение GoldenRATIO помогает разрабатывать веб-сайты, интерфейсы и макеты в соответствии с Золотым Сечением. Оно доступно в Mac App Store за $ 2,99, и имеет встроенный калькулятор с визуальной обратной связью, и удобную функцию «
Золотое сечение. Божественная пропорция | Журнал Ярмарки Мастеров
Золотое сечение (лат. Sectio aurea) — термин, знакомый многим. Освежим немного нашу память, друзья!
Золотое сечение, или золотая пропорция — идеальное соотношение величин, лежащее в основе гармонии природы и человека. «Золотое сечение» имеет массу удивительных свойств (из разряда «Ух, ты! Занимательная геометрия»), возможно, именно поэтому, ему приписывается некое божественное происхождение и ряд вымышленных свойств.
Если выражаться сухо по-научному, то ЗС — это соотношение величин или отрезков, при котором отношение большей части к меньшей равно отношению всей величины к большей части. Приблизительное округленное процентное соотношение частей — 62% и 38%.
Числовая величина золотого сечения – 1, 6180339887 (и это еще округление =)) до десятого знака!)
Пример золотого сечения в лучах пятиконечной звезды.
С Вашего позволения, я опущу многострочные математические фомулы и фомулировки =) Перейдем сразу к Прекрасному!
Зачатки этого понятия встречаются еще в античной литературе, датированной 300 гг. до нашей эры, а «божественная пропорция» широко применялась в трудах и работах мастеров Эпохи Возрождения. Иоган Кеплер, астроном 16 в. назвал золотое сечение одним из сокровищ геометрии. Он впервые обращает внимание то, как проявляется ЗС в ботанике (рост растений и строение стеблей и соцветий).
В середине 19 в. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
На протяжении веков существовало общеприянтое мнение, что рукотворные объекты, созданные с применением принципа ЗС, воспринимаются Человеком как наиболее гармоничные, совершенные. Пропорции золотого сечения можно выделить в проекциях египетских пирамид. Соотношение сторон плана Парфенона в Афинском Акрополе также являет собой не простое кратное число, а бесконечно дробное (догадайтесь, какое?). Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.
Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.
Золотое сечение на примере фасада храма Парфенона
Однако же, бытует и мнение, что значение ЗС в искусстве сильно преувеличенно, порой притянуто за уши исследователями, либо основано наошибочных расчетах. Тут каждый останется при своем. Помню, как на втором курсе в архитектурном нас, лопоухих, профессора пытались приобщить к прекрасному и долго-долго втолковывали про принципы золотого сечения в зодчестве, ряды Фибоначчи и прочее-прочее =)) Но настоящее понимание этой волшебной геометрии пришло ко мне много позже, при изучении бионики (один из стилей архитектуры), которая базируется именно на совершенстве природных форм. Согласитесь, мы не в силах оспаривать очевидное, а примеры идеальной пропорции встречаются сплошь и рядом: в раковинах аммонитов, в расположении ветвей на стебле растения, прожилках листьев.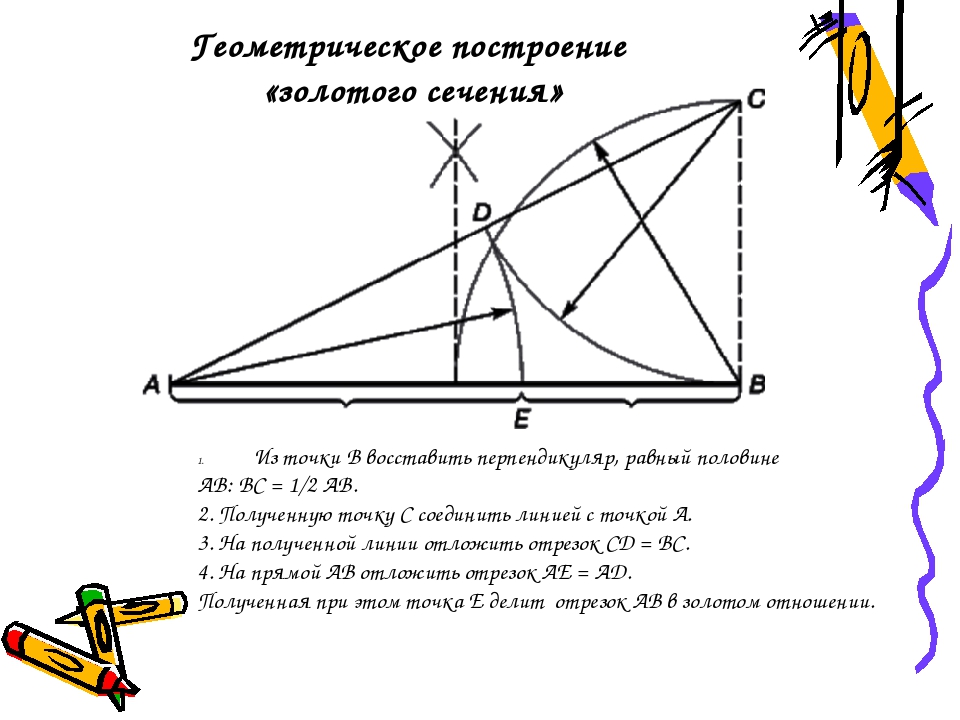
Спираль Архимеда
Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке , семян подсолнечника, шишек сосны проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.
Стебель цикория
Полюбуйтесь, как наглябно иллюстрирует природа принципы Золотого сечения! Совершенные спирали без изъян, соотношения витков которых строго соответсвует канонам и принципам построения ЗС.
© Copyright: Tihomir Balkonskiy
© Copyright: Kibardindesign
Материалы взяты из Интернета.
Текст преимущественно авторский =)
Спасибо за Ваше внимание, Даша Самаркина
Золотое сечение в архитектуре, строительстве, дизайне
Главная » Разное » Правило золотого сечения в архитектуре, строительстве и дизайне
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Содержание статьи
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи.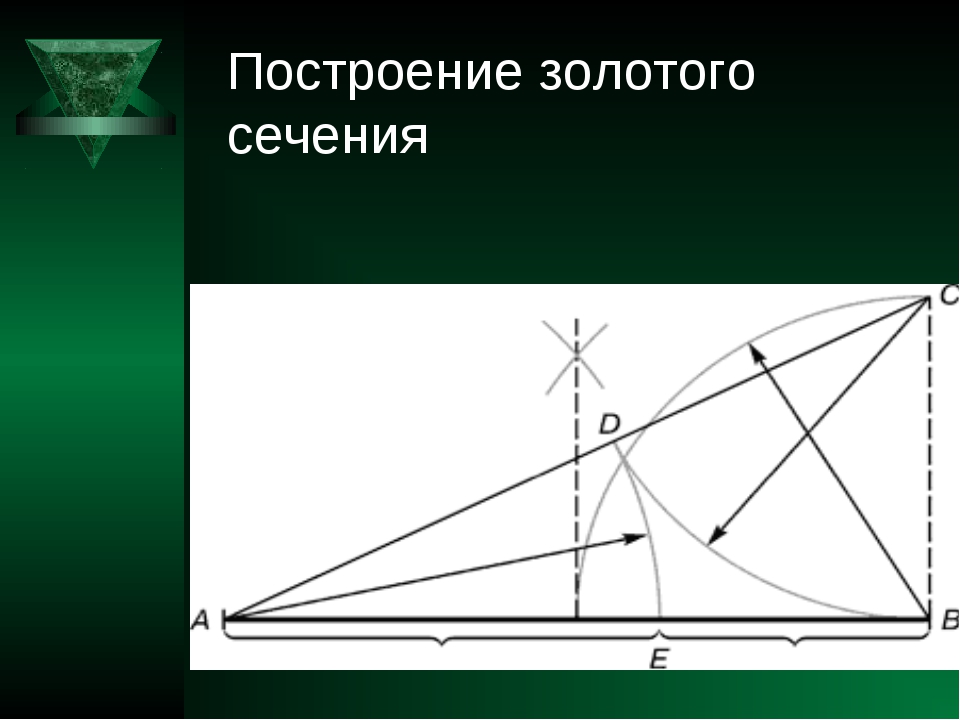 Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Ничего особенного, но взгляд не оторвать. Знаете почему?
Знаете почему?
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D.
 При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C. - Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
Пример подбора цвета по правилам правильной пропорциональности
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты.
 Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
Пропорциональность — важная вещь
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.
Правило треугольника в садовом дизайне
От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Золотое сечение в архитектуре: принцип проектирования зданий
Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.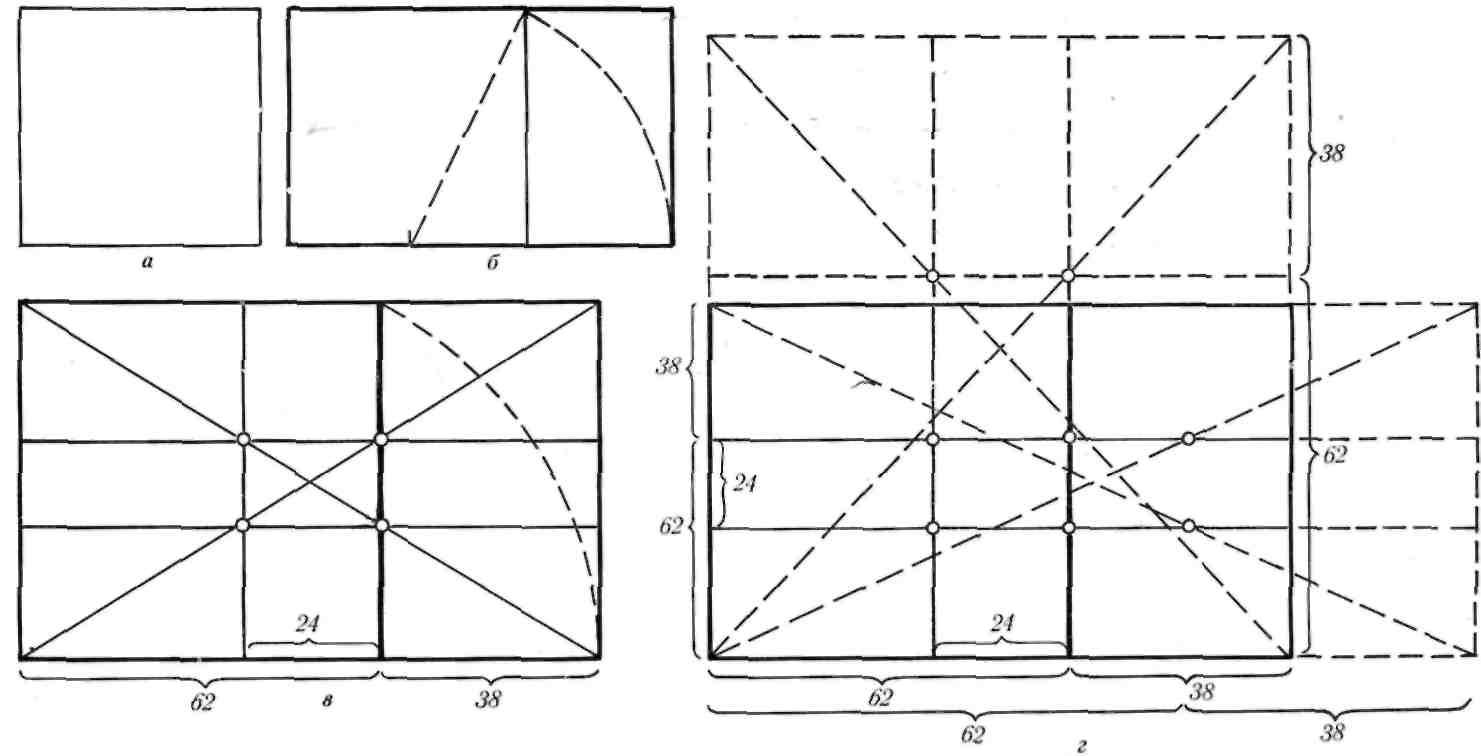
Содержание статьи
Просто о сложном: что это такое – правило золотого сечения
Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.
Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.
Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:
- практически все живые организмы можно привести к принципу числовой зависимости.
 Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию; - данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
- именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.
Экскурс в историю: кто придумал золотое сечение
Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:
- маленький отрезок – это сын;
- большой – отец;
- весь отрезок – это святой дух.
Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.
Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.
Золотое сечение в божественной пропорцииПринцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
Ряд Фибоначчи в церкви Покрова на НерлиКак рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Простой пример золотого сечения в курином яйцеКак построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

На видео можно более подробно узнать про магию чисел Фибоначчи:
Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства
Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.
Тайны древнеегипетской архитектуры
В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.
Это интересно! Форма пирамиды имеет ещё одно неоспоримое свойство.
В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.
Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.
Идеальная пропорция золотого сечения в пирамидеИдеальные пропорции в древней Греции
Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.
Но общие пропорции ЗС соблюдены.
Принцип идеальной пропорции в древнегреческом Парфеноне:
Памятники архитектуры средневековья
Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.
В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участкахАрхитектура России
Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.
Разметчик Фибоначчи построен по правилу золотого сеченияИспользовать циркуль можно практически на любом архитектурном сооруженииЧтобы исследовать большие объекты, нужно отойти на некоторое расстояние и приложить циркульЗолотое сечение в архитектуре Москвы
Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.
В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.
Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.
Кремлевское здание сенатаПречистенский дворецГолицынская больницаДом союзов — благородное собраниеИспользовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам
Дом ПашковаАрхитектура в Санкт-Петербурге
Живым примером золотого сечения является Исаакиевский собор.
ЗС в Исаакиевском собореВ первую очередь можно проанализировать его ширину, равную 400 единицам:
- при делении числа 400 на значение золотого сечения получим приблизительно 248;
- при дальнейшем делении 248/1,618=153;
- основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.

По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.
На фото чётко прослеживаются золотой треугольник и прямоугольник в Исаакиевском собореПриведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.
Кунсткамера
Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.
В башне по всей высоте четко прослеживается равнобедренный треугольник, а это значит, что Кунсткамера построена по общему принципу ЗСТорговый дом Эсдерс и Схейфальс
ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:
- 671, 414, 256, 98, 60, 37 и 23.
Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.
Дом Советов
Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:
- 1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.
Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.
Очевидная пропорциональность Дома СоветовПримеры золотого сечения в современной архитектуре
В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.
Правило золотого сечения при строительстве частного дома
Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.
Что нужно знать при проектировании фасада
В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.
Идеальные пропорции частного домаЗолотое сечение в оформлении интерьера
Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.
Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.
Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:
- 60% — основная палитра;
- 30% — дополнительный оттенок;
- 10% — близкий тон, который усиливает восприятие основного и дополнительного.
Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.
Заключение
Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.
Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.
Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:
Предыдущая
Новинки рынкаОт теории к практике: самостоятельная регулировка окон к зиме
СледующаяНовинки рынкаБалкон и лоджия: в чём разница, о каких нюансах стоит знать, если вы решились на переделку?
Понравилась статья? Сохраните, чтобы не потерять!
ТОЖЕ ИНТЕРЕСНО:
Золотое сечение в: дизайне искусстве природе жизни
Золотое сечение — божественная пропорция: самое загадочное правило дизайна вызывает много споров. Разбираемся, как использовать его, чтобы ваши дизайны выделялись.
Что общего у пирамиды в Гизе и Мона Лизы с логотипом Пепси? И то, и другое создано с помощью золотого сечения. В этой статье мы разберем, что это такое и как его использовать в создании дизайна.
Правило золотого сечения
Золотое сечение — пропорция, которую заметили еще древние египтяне. Чтобы её получить, нужно разделить линию на две части так, чтобы длинная часть соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной. Оказывается, эта пропорция всегда равняется 1,618. Это число еще называют числом «фи».
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками.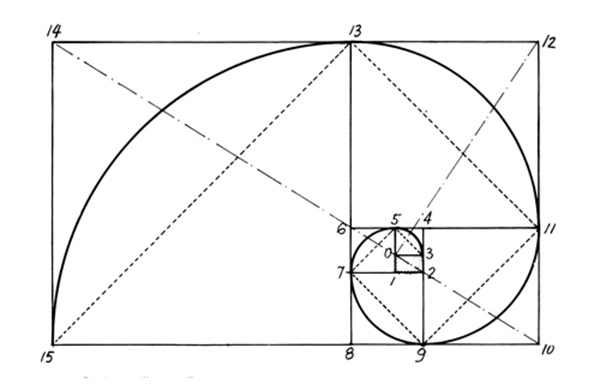 Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.
Ничего особенного, но взгляд не оторвать.
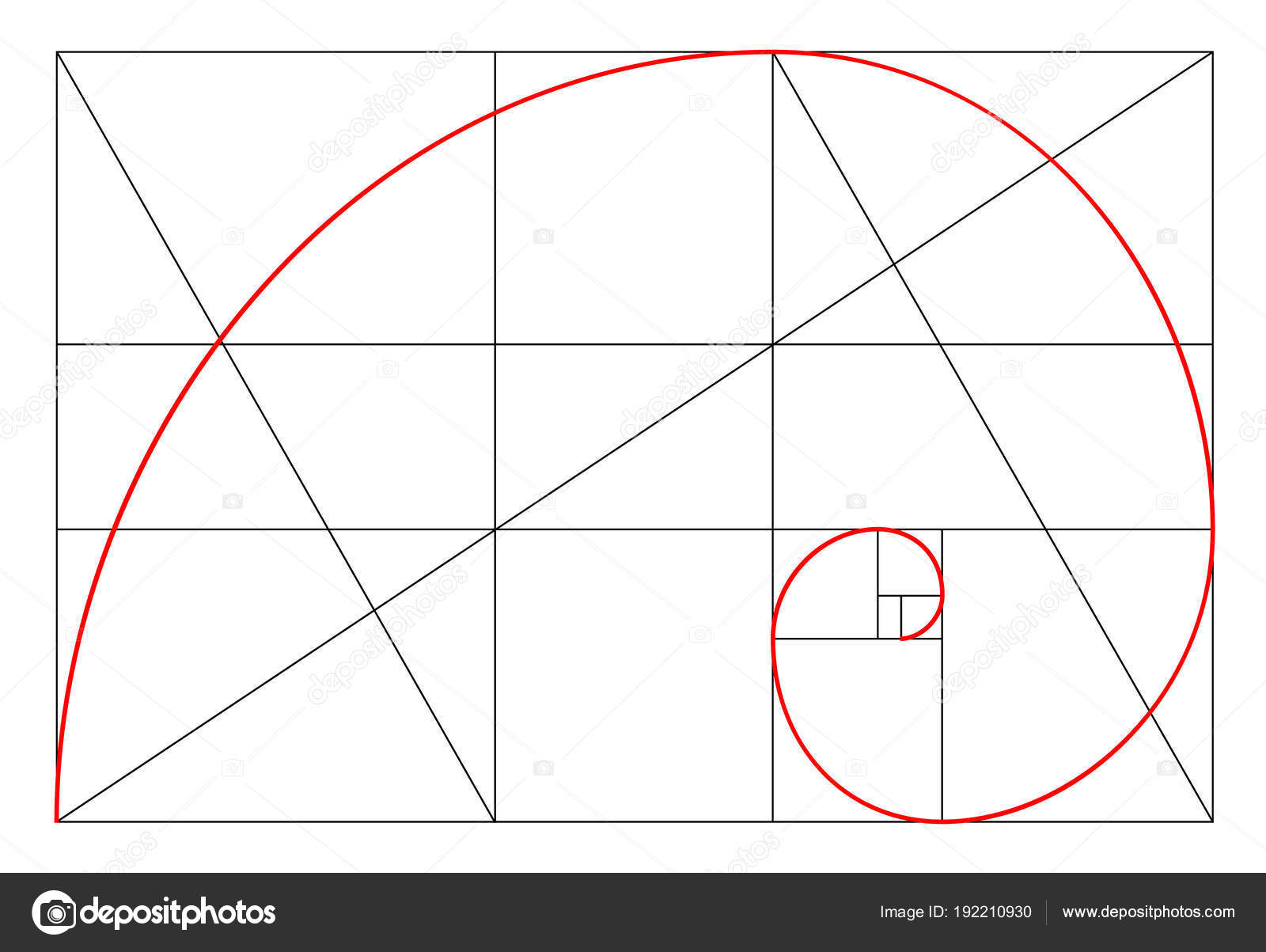 Знаете почему?
Знаете почему?Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.
Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D.
 При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C. - Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много.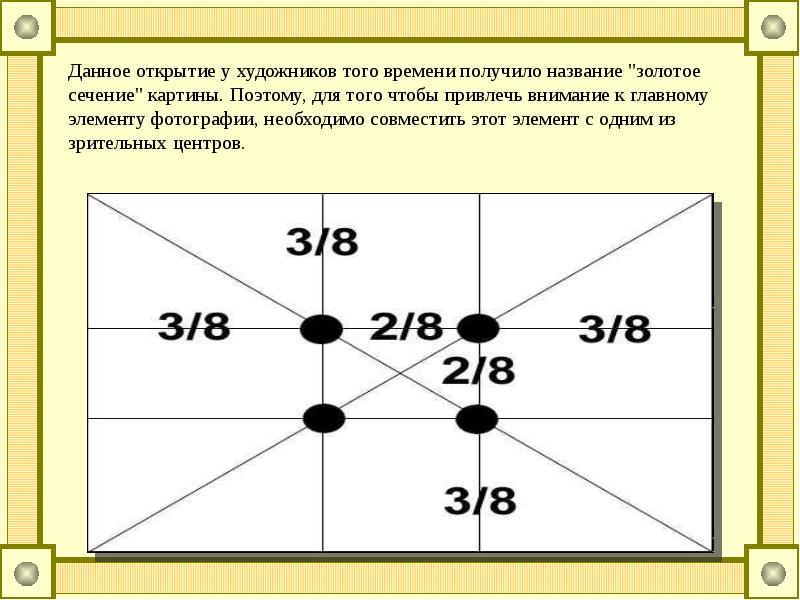 Если рассматривать известные здания, то и там тоже есть та же закономерность.
Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
Пример подбора цвета по правилам правильной пропорциональности - При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
Пропорциональность — важная вещьПочему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.
Правило треугольника в садовом дизайнеОт главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Золотое сечение: пропорция — твойдомстройсервис.рф
Любому человеку, которому хотя бы косвенно приходилось сталкиваться с геометрией пространственных объектов в интерьерном дизайне и архитектуре, строительстве деревянных домов, хорошо известен принцип золотого сечения. Несколько десятков лет назад, популярность золотого сечения была высокой, что сторонники мистических теорий и устройства мира, называют универсальным гармоническим правилом.
Сущность универсальной пропорции
- Большое количество объектов живого мира, от вируса до человека, имеют основные пропорции тела или конечностей, очень близкие к значению золотого сечения;
- Зависимость 0,63 или 1,62 характерна только для биологических существ и некоторых разновидностей кристаллов, неживые объекты, от минералов до элементов ландшафта, обладают геометрией золотого сечения крайне редко;
- Золотые пропорции в строении тела оказались наиболее оптимальными для выживания реальных биологических объектов.
Сегодня золотое сечение находят в строении тела животных, панцирей и раковин моллюсков, пропорций листьев, веток, стволов и корневых систем у достаточно большого числа кустарников и трав.
Многими последователями теории универсальности золотого сечения неоднократно предпринимались попытки доказать тот факт, что его пропорции являются наиболее оптимальными для биологических организмов в условиях их существования.
Обычно в качестве примера приводится устройство раковины Astreae Heliotropium, одного из морских моллюсков. Панцирь представляет собой свернутую спиралью кальцитовую оболочку с геометрией, практически совпадающей с пропорциями золотого сечения.
Более понятным и очевидным примером является обычное куриное яйцо.
Соотношение основных параметров, а именно, большого и малого фокуса, или расстояний от равноудаленных точек поверхности до центра тяжести, будет также соответствовать золотому сечению. При этом форма скорлупы птичьего яйца является наиболее оптимальной для выживания птицы, как биологического вида. При этом прочность скорлупы играет далеко не главную роль.
Золотое сечение, называемое еще универсальной пропорцией геометрии, было получено в результате огромного количества практических измерений и сравнений размеров реальных растений, птиц, животных.
Универсальная пропорция история
О золотой пропорции сечения знали древнегреческие математики Евклид и Пифагор. В одном из памятников древней архитектуры — пирамиде Хеопса соотношение сторон и основания, отдельные элементы и настенные барельефы выполнены в соответствии с универсальной пропорцией.
Методика золотого сечения широко использовалась в средние века художниками и архитекторами, при этом суть универсальной пропорции считалась одной из тайн вселенной и тщательно скрывалась от простого обывателя. Композиция многих картин, скульптур и зданий выстраивалась строго в соответствии с пропорциями золотого сечения.
Впервые суть универсальной пропорции документально была сформулирована в 1509 г монахом-францисканцем Лукой Пачоли, обладавшим блестящими математическими способностями. Но настоящее признание состоялось после проведения немецким ученым Цейзингом всестороннего изучения пропорций и геометрии человеческого тела, древних скульптур, произведений искусства, животных и растений.
У большинства живых объектов некоторые размеры тела подчиняются одним и тем же пропорциям. В 1855 г ученым был сделан вывод о том, что пропорции золотого сечения являются своеобразным стандартом гармонии тела и формы. Речь идет, прежде всего, о живых существах, для мертвой природы золотое сечение встречается значительно реже.
Как получили золотое сечение
Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой. Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.
На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов. Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:
- Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению; - Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
- В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.
Главный секрет золотого сечения
Если природные проявления универсального сечения в пропорциях тел животных и человека, стеблей основы растений еще можно объяснить эволюцией и приспосабливаться к влиянию внешней среды, то открытие золотого сечения в строительстве домов XII-XIX века стало определенной неожиданностью. Мало того, знаменитый древнегреческий Парфенон был построен с соблюдением универсальной пропорции, многие дома и замки состоятельных вельмож и зажиточных людей в средние века строились сознательно с параметрами, очень близкими к золотому сечению.
Золотое сечение в архитектуре
Многие из построек, сохранившихся до сегодняшних дней, свидетельствуют, что архитекторы средневековья знали о существовании золотого сечения, и, конечно, при строительстве дома руководствовались своими примитивными расчетами и зависимостями, с помощью которых пытались добиться максимальной прочности. Особенно проявлялось желание строить максимально красивые и гармоничные дома в постройках резиденций царствующих особ, церквей, ратуш и зданий, имеющих особое социальное значение в обществе. Например, знаменитый собор Парижской богоматери в своих пропорциях имеет немало участков и размерных цепей, соответствующих золотому сечению.
Еще до публикации своих исследований в 1855 году профессором Цейзингом, в конце XVIII века были построены знаменитые архитектурные комплексы Голицынской больницы и здания сената в Санкт-Петербурге, дома Пашкова и Петровского дворца в Москве с использованием пропорций золотого сечения.
Разумеется, дома с точным соблюдением правила золотого сечения строили и ранее. Стоит упомянуть памятник древней архитектуры церкви Покрова на Нерли, изображенный на схеме. Всех их объединяет не только гармоничное сочетание форм и высокое качество строительства, но и, в первую очередь, наличие золотого сечения в пропорциях здания. Удивительная красота постройки становится еще более загадочной, если принять во внимание возраст, здание церкви Покрова датируется XIII веком, но современный архитектурный облик постройка получила на рубеже XVII века в результате реставрации и перестройки.
Особенности золотого сечения
Старинная архитектура зданий и домов средневековья остается притягательной и интересной для современного человека по многим причинам:
- Индивидуальный художественный стиль в оформлении фасадов позволяет избежать современного штампа и серости, каждое здание представляет собой произведение искусства;
- Массовое использование для декорирования и украшения статуй, скульптур, лепнины, необычных сочетаний строительных решений разных эпох;
- Пропорции и композиции здания притягивают взор к наиболее важным элементам постройки.
Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах. Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению.
Поэтому современная наука считает, что феномен универсальной пропорции является психологическим явлением, а не действием каких-либо метафизических сил.
Использование в дизайне и архитектуре
Принципы применения золотой пропорции в последние несколько лет стали необыкновенно популярны в строительстве частных домов. На смену экологии и безопасности строительных материалов пришли гармоничность конструкции и правильное распределение энергии внутри дома.
Современная интерпретация правила всеобщей гармонии давно распространилась за пределы привычной геометрии и формы объекта. Сегодня правилу подчиняются не только размерные цепи длины портика и фронтона, отдельных элементов фасада и высоты здания, но и площадь комнат, оконных и дверных проемов, и даже цветовая гамма внутреннего интерьера помещения.
Проще всего построить гармоничный дом на модульной основе. В этом случае большинство отделений и комнат изготавливаются в виде самостоятельных блоков или модулей, спроектированных с соблюдением правила золотого сечения. Построить здание в виде набора гармоничных модулей значительно проще, чем строить одну коробку, в которой большая часть фасада и внутренних помещений должна быть в жестких рамках пропорций золотого сечения.
Немало строительных фирм, выполняющих проектирование частных деревянных домов из бревна, лафета, бруса используют принципы и понятия золотого сечения для сметы и глубокой проработки конструкции дома бревенчатого. Как правило, такой дом из сруба очень удобный и гармоничный в пользовании. Правильно подобранное соотношение площадей комнат гарантирует душевный комфорт и отменное здоровье хозяев.
Если дом срубовой был построен без учета оптимальных соотношений золотого сечения, можно выполнить перепланировку комнат так, чтобы пропорции помещения соответствовали соотношению стен в пропорции . Для этого может перемещаться мебель или устанавливаться дополнительные перегородки внутри комнат. Аналогичным образом меняются размеры оконных и дверных проемов так, чтобы ширина проема была меньше высоты дверного полотна . Таким же способом выполняется планирование мебели, бытовой техники, отделки стен и пола.
Сложнее выбрать цветовое оформление. В этом случае вместо привычного соотношения последователями золотого правила принята упрощенная трактовка . То есть основной цветовой фон должен занимать 60% пространства помещения, оттеняющему цвету отдают не более 30%, и остальное отводится под различные родственные тона, призванные усилить восприятие цветового решения.
Внутренние стены помещения делятся горизонтальным поясом или бордюром на высоте 90 см, установленная мебель должна соизмеряться с высотой потолков по соотношению золотого сечения. То же правило касается распределения длин, например, размер дивана не должен превышать 2/3 длины простенка, а общая площадь, занимаемая мебелью, относится к площади комнаты.
Золотую пропорцию сложно в массовом порядке применять на практике из-за всего лишь одного значения сечения, поэтому при проектировании гармоничных зданий нередко прибегают к ряду чисел Фибоначчи. Это позволяет расширить количество возможных вариантов пропорций и геометрических форм основных элементов дома. В этом случае ряд чисел Фибоначчи, связанных между собой четкой математической зависимостью, называют гармоническим или золотым.
В современной методике проектирования жилья на основе принципа золотого сечения, кроме ряда Фибоначчи, широко используется принцип, предложенный известным французским архитектором Ле Корбюзье. В этом случае в качестве отправной единицы измерения, по которой рассчитываются все параметры здания и внутреннего интерьера, выбирается рост будущего владельца или средняя высота человека. Такой подход позволяет спроектировать дом не только гармоничный, но и по-настоящему индивидуальный.
Подведём итоги
На практике, по отзывам тех, кто решился на строительство дома из сруба бревенчатого,кирпича или иных строительных материалов по правилу золотого сечения, качественно построенный бревенчатый дом действительно оказывается достаточно удобным для проживания. Но стоимость строения из-за индивидуального проектирования и применения стройматериалов нестандартных размеров возрастает . И в этом подходе нет ничего нового, так как большинство срубовых домов,зданий,строений прошлого века строилось именно под индивидуальные особенности будущих хозяев.
Действительно ли работает золотое сечение Адониса? Наш обзор.
Журнал Men’s Health назвал золотое сечение «Формулой идеального тела». Итак, как это странное открытие действительно работает для всех типов телосложения?
Хорошо, так что это?
Золотое сечение Адониса — это 12-недельная система, которая разделена на три 4-недельных цикла. Он основан на научном факте, что мы созданы, чтобы находить определенную форму тела гораздо более привлекательной. Это золотое сечение .
Эту полностью адаптируемую программу тренировок можно применять независимо от вашего возраста или текущего плана тренировок . Это потому, что он будет учитывать вашу личную ДНК и, следовательно, тип телосложения.
Таким образом, вы можете адаптировать программу тренировок и питания, чтобы сжигать жир для получения энергии и наращивать сухую мышечную массу с максимально возможной скоростью.
Что такое золотое сечение?
Вам знакомы первые впечатления от людей? Это большая его часть.
Когда мужчины достигают этой формы (а это может сделать любой, потому что речь идет о пропорциях, а не о «больших»), это вызывает более высокий уровень привлекательности со стороны женщин и большего уважения со стороны мужчин! И все это происходит в течение первых 4 секунд встречи с кем-то, даже не зная почему.
Но это даже больше. Потому что, когда ваше тело имеет это идеальное соотношение плеч и талии, становится легче избавляться от жира, наращивать мышцы и работать лучше. Ваше тело приобретает естественную форму, задуманную природой.
Итак, программа обучения Золотому сечению Адониса сосредоточена на том, чтобы показать вам, как быстро достичь, а затем сохранить это «золотое сечение».
И это делается с учетом того, что существует много разных типов телосложения. Гибкость системы позволяет вам адаптировать программу обучения не «для всех», а специально для вас.
Примечание: Мы надеемся, что вам нравятся продукты, которые мы рекомендуем на этом сайте, так же, как и нам. Но, чтобы вы знали, наш сайт может получать небольшую комиссию за реферал, если вы решите совершить покупку, перейдя по ссылке на этом сайте.Это не влияет на цену, которую вы платите, или на наше мнение о каких-либо продуктах.
Кто стоит за программой золотого сечения Адониса?
Его создал Джон Барбан с помощью Кайла Леона. Вы не знаете Джона, но было бы довольно сложно найти кого-нибудь более квалифицированного для создания этой системы. Помимо 10 лет, которые он провел в качестве ТОЛЬКО консультанта по большей части индустрии спортивных добавок, он также преподает человеческую эффективность в Университете Флориды.
Посмотрите видео здесь, чтобы узнать больше о науке и этой программе: —
И когда вы видите, в какой форме он находится, вы знаете, что он практикует именно то, чему учит!
Итак, после своего многолетнего опыта и усердного обучения, он разработал эту систему специально, чтобы дать вам идеальный тонус и пропорции тела за безумные 12 недель.
Что вы получаете?
При покупке Золотого сечения Адониса вы получите полностью загружаемую программу тренировок. Это означает, что вы можете мгновенно загрузить полную 12-недельную систему. Это круто, не нужно ждать доставки!
Внутри вы найдете подробную информацию о том, какие типы упражнений вам следует делать, и , что не менее важно, упражнения, которых следует ИЗБЕГАТЬ. . Те мертвые подъемы и скручивания пресса с отягощением, которые вы делали, — плохая идея, — говорит Джон, и он объяснит вам, почему.
Всего 78 продвинутых видеоуроков, составляющих руководство по тренировкам и фитнесу. Они четко объясняют, как совершенствовать свои техники, чтобы вы получали максимальную пользу от каждой завершенной тренировки.
Nutritional Software
Все мы знаем, что «вы то, что вы едите» и т.д. помогает. Да, есть такое понятие, как избыток белка.
Это подробное руководство по питанию расскажет, как улучшить и настроить свой рацион в соответствии с вашим личным «индексом Адониса». Это также простая в использовании кнопка, так что не думайте, что эта часть пакета собирает для вас всю техническую информацию 🙂
Руководство по дополнениям
Это руководство отличается от любой другой информации о дополнениях, которую вы когда-либо читали.
Помните, это исходит от парня, к которому производители пищевых добавок обращаются за советом.
На индустрию спортивных добавок потрачено много денег.И большинство этих компаний хотят ваших денег, не заботясь о ваших реальных результатах.
Как говорит Джон, 9 из 10 протеиновых добавок — пустая трата денег . И он нашел только 1 жиросжигатель, который может пригодиться (держу пари, что вы никогда не слышали об этом, когда он тоже рассказывает вам, что в нем содержится!).
Все это конечно возмутительно. Но именно поэтому Джон теперь доверяет только двум брендам (он также показывает вам хитрый трюк, чтобы сэкономить и на них).
Это подходит для всех?
Самое замечательное в этом подходе к обучению то, что он действительно адаптирован под вас индивидуально.Ваш тип телосложения и генетический состав являются важнейшим фактором в достижении результатов, поэтому любая программа, не учитывающая этого, обрекает вас на провал.
Конечно, есть одна вещь, о которой следует помнить.
Не думайте, что это будет прогулка по парку! Если вы действительно хотите иметь тело AGR, это вызовет вам трудности. Но мы с вами знаем, что любая система тренировок, которая утверждает, что она «легкая», не является честной — и в конечном итоге не будет работать.
И, конечно же, если вы еще не тренируетесь или тренируетесь, не ожидайте, что это сработает, не приложив больших усилий.Вы ведь хотите больших результатов? Они не придут, если вы просто посмотрите видео и ничего не сделаете 🙂
И хотя этот всеобъемлющий пакет подходит для всех, независимо от того, какой у вас сейчас размер или форма — если вы в довольно плохой форме, вам, конечно, следует поговорить Обратитесь к врачу, прежде чем приступить к занятиям фитнесом.
Сколько это стоит?
Вы, наверное, ожидаете здесь цифры в сотни. Но на самом деле полный пакет обучения обойдется вам всего в 37 долларов.Это все, включая программное обеспечение для питания. Они также добавляют некоторые изящные дополнительные бонусы (см. Ниже). А поскольку все это мгновенная загрузка, тоже не нужно платить за доставку.
Я надеюсь, что они сохранят эту цену, потому что, честно говоря, они могут взимать гораздо больше, так что это немного воровство. Но не говорите им, что я сказал, что 🙂
100% гарантия возврата денег
Вам это все равно не понадобится, но приятно знать, что они действительно поддерживают свой продукт. На самом деле они дают вам чертовски щедрые 60 дней, чтобы попробовать все.
Попробовать, не нравится? Просто спросите, и вы получите полный возврат средств (я точно знаю, что они тоже поддерживают это!). Так что, если вы не уверены, считайте это безрисковым .
Получите программу прямо с официального сайта Kyle & John здесь — мгновенная загрузка
Некоторые дополнительные бонусы
Сама основная программа — это все, что вам действительно нужно. Но они добавляют некоторые дополнительные бонусы, о которых я должен упомянуть, потому что они вам тоже понравятся 🙂
Во-первых, вы получаете пожизненных обновлений БЕСПЛАТНО основного пакета.Это означает, что когда они добавляют что-то новое или улучшают это — вы тоже получаете эти обновления без дополнительной оплаты, на всю жизнь. Довольно круто и совсем не ожидаемо (кто еще это делает!).
Тогда есть дополнительное руководство для тех, кто ищет «усилитель пресса и рук» — имеет смысл, кто не хочет больших рук и лучшего пресса. Предупреждаю, хотя это сложная программа, но если вы хотите быть крупнее, вам это понравится.
И, наконец, бонус не от Джона Барбана. Это немного по-другому, и это было не в моем вкусе.Все дело в том, чтобы ваше тело выглядело значительно лучше безумно быстро с помощью хитрых уловок с водой / углеводами. Это тот материал, который используют бодибилдеры на соревнованиях, поэтому он работает. Но, как я уже сказал, мне не нравятся такие вещи, но другим обзорам Золотого сечения Адониса это понравилось. И в любом случае это интересное чтение, и оно бесплатное, так что особо не жалуюсь.
В заключение
Хорошо, так что стоит ли покупать?
Это действительно комплексная система, которая занимает всего 12 недель.(Просто взгляните на некоторые из фотографий до и после на их веб-сайте ниже)
Это поможет вам быстро понять генетический состав вашего тела. И как только это будет понято, вы сможете ставить перед собой цели.
Он дает советы экспертов мирового класса по питанию и добавкам, которые многие другие программы игнорируют или просто ошибаются. Невозможно переоценить важность правильного питания при наращивании мышечной массы — вы можете работать сколько угодно, но сделайте это неправильно, и ваши результаты будут совершенно отстойными (были там, сделали это!).
И все это поставляется в виде пакета мгновенной загрузки , к которому вы можете получить немедленный доступ. По цене, которую я могу назвать лишь небольшой выгодной сделкой (меньше, чем цена подписки на фитнес-журнал, которая полна путаницы и множества рекламных объявлений!).
Так что, если вы когда-нибудь обнаруживали, что ваши тренировки не позволяют достичь того, что, по вашему мнению, они должны, это для вас. Или, если вы еще даже не начали, но не хотите оглядываться на пару лет назад, задаваясь вопросом, почему все эти усилия не сработали почти так хорошо, как сказал тренер, начните сейчас с системы, основанной на реальных наука.
Где его взять?
Эта программа доступна онлайн только напрямую от Кайла и Джона. Вы не можете купить его ни на Amazon, ни в местных магазинах.
Получите программу прямо с официального сайта Kyle & John здесь — мгновенная загрузка
Дополнительная информация
Для более подробного объяснения науки и того, что включает в себя курс, это видео от Kyle должно помочь ответить на любые вопросы: —
Логотип Apple Park — Как строить с использованием золотого сечения
Увидев логотип Apple Park и расположение на нем концентрических колец, я решил, что он основан на сетке Apple.
Джони Айвз упомянул систему сеток при представлении iOS 7 и сетку значков iOS. Сетка значков iOS и система сеток — это не одно и то же. Сетка, похоже, основана на геометрической прогрессии Сэмюэля Колмана 19 века и динамической симметрии.
Золотое соотношение и коэффициент корня-два
Сетка значков iOS использует две пропорции; золотое сечение (золотая пропорция) и пропорция корня два. Третья пропорция в системе — это тройной корень.Вы можете найти пропорцию root-three в значках системных настроек tvOS и MacOS. Пошаговые инструкции по созданию сетки значков для tvOS и MacOS см. В разделе «Дизайн значков».
Сетка значков iOS
Сетка значков iOS казалась логичным местом для воссоздания логотипа Apple Park. Я использую Affinity Designer, чтобы нарисовать это. Вы сможете следовать этим инструкциям с помощью Adobe Illustrator.
Шаг 1) Используя горизонтальную граничную линию сетки, нарисуйте первое кольцо логотипа Apple Park.Совместите ход этого кольца с внутренней стороной. Я установил толщину линии 5pt.
Шаг 2) Нарисуйте круг с центром в окружности средней окружности iOS Icon Grid с радиусом, заданным окружностью самого маленького круга.
Шаг 3) Используя окружность фиолетового круга, нарисованного на шаге 2, чтобы задать диаметр кольца, нарисуйте второе кольцо с логотипом. Совместите ход этого кольца с внешней стороной.
Так как это проще, я перейду к созданию набора золотых прямоугольников. Я буду использовать их, как линейки, чтобы установить радиусы оставшихся колец.
Шаг 4) Создайте набор из четырех вложенных золотых прямоугольников, где высота первого прямоугольника (желтого цвета) задается окружностью круга, созданного на шаге 2, и горизонтальной линией сетки значка iOS, как показано ниже.
Примечание. Желтый прямоугольник частично скрыт другими прямоугольниками.Розовые точки показывают высоту желтого прямоугольника.
Шаг 5) Сделайте копии большого желтого прямоугольника и маленького красного прямоугольника и разложите их, как показано ниже.
Примечание: оранжевый и фиолетовый прямоугольники не нужны. Их можно удалить.
Шаг 6) Нарисуйте следующие два кольца с логотипом Apple Park. Совместите ход этих колец с центром.
Шаг 6) Нарисуйте широкую полосу, используя высоту самых маленьких прямоугольников, чтобы задать внутренний и внешний радиусы полосы.
Создание логотипа Apple Park
Теперь, когда сетка удалена, готовый логотип. Бьюсь об заклад, вы не ожидали, что ему будет легко.
Если вы заинтересованы в создании логотипов в виде концентрических кругов с использованием геометрических прогрессий, посмотрите мой последний урок по Skillshare.
Надеюсь, вам понравилось это пошаговое руководство. Не забудьте посетить этот класс, если у вас будет возможность, и мою книгу по дизайну иконок.
Нравится:
Нравится Загрузка …
Золотое сечение и числа Фибоначчи
Золотое сечение и числа ФибоначчиЗолотое сечение () — это иррациональное число с несколькими любопытными свойствами. Его можно определить как число, равное своему обратному значению плюс один: = 1 / + 1 . Умножая обе части этого же уравнения на золотое сечение, мы получаем интересное свойство: квадрат золотого сечения равен самому простому числу плюс один: 2 = +1 .Поскольку это уравнение можно записать как 2 — — 1 = 0 , мы можем получить значение золотого сечения из квадратного уравнения, где a = 1 , b = -1 и c = -1 :. Золотое сечение — это иррациональное число, но не трансцендентное (как), поскольку оно является решением полиномиального уравнения.
Это дает нам либо 1,618 033 989 , либо -0,618 033 989 . Первое число обычно рассматривается как само золотое сечение, второе — как отрицательное значение его обратной величины — или мы можем использовать второе само по себе, как число «,», которое будет использоваться ниже.Золотое сечение можно также получить из тригонометических функций: = 2 sin 3/10 = 2 cos / 5 ; и 1 / = 2 sin / 10 = 2 cos 2/5 . Углы в тригонометрических уравнениях в градусах, а не в радианах, равны 54 o , 36 o , 18 o и 72 o соответственно.
Золотое сечение, кажется, получило свое название от Golden Rectangle , прямоугольника, стороны которого пропорциональны золотому сечению.Теория Золотого Прямоугольника — эстетическая, что соотношение является эстетически приятным и поэтому может быть обнаружено спонтанно или намеренно в большом количестве произведений искусства. Так, например, фасад Парфенона можно удобно обрамить золотым прямоугольником.
Насколько приятен золотой прямоугольник, как часто он действительно появляется в искусстве и действительно ли он обрамляет фасад Парфенона, может быть во многом вопросом интерпретации и предпочтений.Однако построение золотого прямоугольника — интересное упражнение в геометрии золотого сечения, как показано справа. Начиная с единичного квадрата, сначала квадрат делится пополам, затем в полуквадрате проводится диагональ. Длину диагонали можно рассчитать с помощью теоремы Пифагорана, основанной на треугольнике, который составляет ,5 с одной стороны и 1 с другой. Таким образом, диагональ равна (1 + 0,5 2 ) = (1,25) = 1,118033989 . Если мы просто добавим .5 , получается золотое сечение, 1,6l8033989 . Таким образом, если мы расширим сторону единичного квадрата и нарисуем круг с радиусом диагонали и его центром в средней точке на единичной стороне, круг будет пересекать сторону в точке, которая будет на 1,6 л8033989 единиц от угла. площади. Фактически, это дает нам уравнение для золотого сечения: = 0,5 + 1,25 . Однако мы можем легко превратить это в предыдущее уравнение, просто умножив числа, чтобы получить целые числа: = 1/2 + 21.25/2 = (1 + 21,25) / 2 = (1 + (4 * 1,25)) / 2 = (1 + 5) / 2 .
Независимо от того, имеют ли золотое сечение или золотой прямоугольник эстетическое значение, соотношение действительно имеет важное значение в задачах естественной симметрии. Например, поверхность может быть полностью и симметрично выложена плиткой из треугольников, квадратов и шестиугольников, но не пятиугольников. Периодическая пятикратная симметрия в природе не встречается. Однако в начале 70-х годов Роджер Пенроуз обнаружил, что поверхность может быть полностью облицована асимметричным и непериодическим способом всего двумя формами, называемыми «воздушными змеями» и «дротиками» — «плитками Пенроуза» — как показано на верно.Однако внутри этой мозаики могут быть небольшие области пятикратной симметрии. Может появиться несколько декагонов, некоторые из которых на расстоянии могут выглядеть как пятиугольники.
Так уж получилось, что, учитывая достаточно большую площадь, соотношение воздушных змеев и дротиков составляет всего , золотое сечение . Почему это могло произойти? Итак, полный круговой угол (360 o ), деленный на пять, равен 72 o , что произошло выше как один из углов, тригонометрическая функция которых — золотое сечение.Что еще более заметно, сама иррациональность золотого сечения является артефактом квадратного корня из пяти:. Если золотое сечение встречается в примерах пятикратной симметрии, это вполне может быть связано с тем, что само число фундаментально связано с числом пять.
Теперь числа Фибоначчи встречаются в природе.Спирали, видимые в головке ромашки, состоят из отдельных «цветочков», которые считаются числами Фибоначчи. Здесь это важно, потому что соотношение между любыми двумя последовательными числами Фибоначчи приближается к пределу , когда числа становятся больше, и этот предел составляет золотого сечения . Таким образом, 6765/4181 (20-й и 19-й уровни Фибоначчи) равно 1,618033963, что отличается от золотого сечения только на 0,000000025 .
Таблица справа иллюстрирует интересный способ естественного появления чисел Фибоначчи по отношению к золотому сечению.Это основано на уже отмеченном выше свойстве золотого сечения: 2 = +1 . Точно так же любую степень золотого сечения можно разбить на сумму меньших степеней, например, 5 = 4 + 3 . Из-за этого любая степень золотого сечения может быть в конечном итоге уменьшена до суммы , целого числа и целого числа , кратного золотого сечения. Пример прохождения всего этого процесса для большой державы приведен в сноске.Любопытно, что все эти целые числа оказались числами Фибоначчи . Таким образом, 7 равно 13 + 8 . Это можно обобщить, так что для каждой степени:
n = f n + f n-1 .
Поскольку, как мы видели выше, существует два решения квадратного уравнения для, также верно, что n = f n + f n-1 .Если вычесть одно уравнение из другого, мы получим интересный результат:
n = f n + f n-1
— ( n = f n + f n-1 )
_______________
n — n = f n (-) ,
или f n = ( n — n ) / (-) .Если вернуться к квадратному уравнению,
— = (1 + 5) / 2 — (1 — 5) / 2 = 5 . Таким образом, мы получаем общее уравнение для чисел Фибоначчи: f n = ( n — n ) / 5 . При использовании этого уравнения необходимо следить за тем, чтобы число на самом деле было отрицательным, и поэтому оно становится отрицательным или положительным в зависимости от степени, в которую оно возведено. Это формула « Бине, », названная в честь математика Жака Бине.
Хотя мы видим, что ряд Фибоначчи естественным образом возникает при оценке степеней золотого сечения, это не обязательно проясняет, почему отношение членов ряда Фибоначчи должно приближаться к золотому сечению как пределу.Как это случается, связь может быть проиллюстрирована с помощью техники непрерывных дробей , которая представляет собой устройство для сокращения неповторяющихся десятичных дробей до дробей, то есть до отношений целых чисел. Техника сокращения повторяющихся десятичных знаков до дробей обсуждалась в другом месте. При неповторяющихся десятичных дробях целая часть числа последовательно удаляется, а из оставшейся десятичной дроби берется обратная величина , в результате чего получается новое целое число, которое затем удаляется, и процесс повторяется.Это может продолжаться до тех пор, пока не будет достигнута желаемая точность или мощность калькулятора не будет превышена — поскольку я предполагаю, что большинство людей сегодня будет использовать калькулятор для получения обратных величин (в противном случае это не очень удобная процедура). Как только получено достаточное количество целых чисел, соответствующая дробь со всеми вложенными дробями может быть решена для простой целочисленной дроби.
Например, справа показана непрерывная дробь для отношения продолжительности лунного (синодического) месяца (29.530588 дней), а продолжительность солнечного (тропического) года (365,24219878 дней). Это говорит нам о количестве лунных месяцев в солнечном году; а в целочисленной форме дробная часть сообщит нам, сколько дополнительных лунных месяцев (более 12 в год) нужно добавить в определенный период солнечных лет, чтобы приблизиться к истинному соотношению. Истинное соотношение — 12,368267058. Удаление 12, а затем последовательное взятие обратного и удаление целой части снова дает нам целые числа после 12, 2, 1, 2, 1, 1 и 17 (по крайней мере).Последовательные приближения могут быть сделаны, останавливаясь на каждом новом целом числе. Таким образом, имея только 2 , мы будем иметь приближение 12 + 1/2 . Остановка со следующим 1 , 1 добавляется к 2 , и следующее приближение равно 12 + 1/3 . Добавление следующего числа, 2 , дает долю 3/8 , что исторически очень важно, потому что популярное древнее устройство для приближения лунного календаря к солнечному году должно было добавлять 3 дополнительных месяца каждые 8 лет. .Однако более важным было дробление на два шага дальше. Добавление 7 лунных месяцев каждые 19 лет было приемом, принятым в Вавилонском календаре. Это правило было унаследовано и используется даже сегодня по еврейскому календарю и христианскому исчислению Пасхи. Следующая дробь в серии, 123/334 , слишком велика, чтобы ее можно было использовать в календарных целях. (Непрерывная дробь для приведена в сноске.)
Золотое сечение обладает уникальным свойством: его обратная величина всегда дает одно и то же десятичное число , а обратная десятичная дробь всегда дает целое число 1 .Это означает, что непрерывную дробь можно построить, не заморачиваясь с калькулятором! Непрерывная дробь однозначно содержит только 1 . Это также означает, что последовательные дроби могут быть получены без обращения к диаграмме. Для каждой дроби мы добавляем 1 , а затем переворачиваем ее (делаем обратное) для каждой новой дроби. Таким образом, первое число — 1 , что дает дробь 1/1 . Это само по себе обратное. К этому добавляется 1 ( 1/1 ), в результате получается дробь 2/1 .Обратной величиной будет 1/2 , наша вторая дробь. К этому снова добавляется 1 (теперь 2/2 ), в результате получается дробь 3/2 . Обратное значение — 2/3 , наша третья дробь. К этому снова добавляется 1 (теперь 3/3 ), в результате получается дробь 5/3 . Обратная величина — 3/5 , наша четвертая дробь. По мере того, как это продолжается, мы можем заметить, что процедура генерирует дроби, которые все состоят из последовательных чисел Фибоначчи ! Вот почему отношения чисел Фибоначчи приближаются к золотому сечению, все они представляют собой решения уникальной непрерывной дроби для золотого сечения!
Я получил от Девина Чалмерса из Джуно, штат Аляска, вывод непосредственно из определения ряда Фибоначчи (уравнение 1 ).Уравнение 2 перемещает определение над одним в ряду; затем мы делим обе стороны на a (n) в уравнении 3 , которое мы обрабатываем с помощью алгебры. Предел обоих соотношений в уравнении 4 должен быть одним и тем же числом, поэтому мы заменяем их переменной в уравнении 5 . Это эквивалентно уравнению 6 , которое, как мы видели выше, можно подставить в квадратное уравнение, чтобы получить уравнение 7 .
Таким образом, хотя золотое сечение не так важно, как другие математические константы, оно претендует на известность и имеет свои собственные уникальные свойства.И, если подумать еще раз, мы действительно можем превратить это в очень серьезную компанию. Таким образом, если мы определим золотое сечение как число, которое при вычитании на равно его собственному обратному ( — 1 = 1/), мы могли бы в свою очередь спросить, какое число, если умножить на минус единица равна своей собственной обратной величине ( x * -1 = 1 / x ). Оказывается, это мнимое число , i = -1: — i = l / i .Это гораздо более значимое и загадочное число, чем золотое сечение — неплохое, как своего рода кузен.
Философия науки, математика
Философия науки
Домашняя страница
Авторское право (c) 1999, 2003, 2008, 2011, 2012, 2019 Келли Л. Росс, доктор философии Все права защищены
Золотое сечение и числа Фибоначчи, Примечание 1
Вернуться к тексту
Золотое сечение и числа Фибоначчи, Примечание 2;
Непрерывная дробь для числа Пи
Непрерывная дробь для представляет некоторый интерес, потому что греки пытаются вывести значение для всегда давали его в форме дроби — у древних не было десятичной записи.Лучшее, что они могли сделать, согласно Айзеку Азимову («Часть Пи», 1964), было 22/7 , что является лишь самой маленькой дробью в ряду (конечно, после 3/1 ). Архимед обнаружил, что число меньше 22/7 и больше 223/71 , но этого все еще недостаточно, чтобы найти следующую дробь в ряду. Только в 16 веке было обнаружено значение 355/113 . Как видите, на самом деле это лучшее, что можно сделать с относительно простой дробью, и современные математики в любом случае имеют новые обозначения и методы для решения этой задачи, не продолжая вообще определять дробь.Однако следующая пара дробей в серии дает чрезвычайно точные значения. 104,348 / 33,215 отличается от только на 1 / 3,030,303,030 ; и 103,993 / 33,102 отличается только на 1 / 1,724,137,931 . Для сравнения: 355/113 отличается от на 1 / 3,748,688 ; 333/106 по 1/12 016 ; и 22/7 по 1/791 . Таким образом, легко удовлетворяется любое желание получить целочисленные значения в широком диапазоне точности.
Вернуться к тексту золотого сечения
Текст непрерывной дроби синодического месяца
Философия науки
Домашняя страница
Copyright (c) 1999 Келли Л. Росс, доктор философии Все права защищены
φ, золотое сечение | ScienceBlogs
Многие люди просили меня написать о φ, золотом сечении. Я наконец сдаюсь и делаю это. Я не большой поклонник φ. Это номер
, который был принят всевозможными сумасшедшими и сумасшедшими, и есть предполагаемые наблюдения его во всевозможных странных местах, которые просто * не * реальны.Например, гагары-пирамиды утверждают, что великие пирамиды в Египте имеют пропорции, которые происходят от φ, но это не так. Мистики животных утверждают, что соотношение трутней к личинкам в улье приблизительно равно φ, но это не так.
Но это интересное число. Моя личная причина думать, что это круто, носит репрезентативный характер: если вы запишете φ в виде непрерывной дроби, это будет [1; 1,1,1,1 …]; и если вы запишете его как непрерывный квадратный корень, это 1 + sqrt (1 + sqrt (1 + sqrt (1 + sqrt (1 …)))).
Что такое φ?
——————
φ — это величина так называемого «золотого сечения»: это число, которое является решением уравнения (a + b) / a = (a / b).(1 + sqrt (5)) / 2. Это соотношение, при котором если вы возьмете прямоугольник, у которого отношение длин сторон равно 1: φ, то, если вы удалите из него максимально возможный квадрат, вы получите еще один прямоугольник, стороны которого имеют соотношение φ: 1. Если вы возьмете из него самый большой квадрат, вы получите прямоугольник, стороны которого имеют отношение 1: φ. И так далее:
Предположительно, это пропорция сторон прямоугольника, обеспечивающая наиболее эстетичный вид. Я недостаточно художник, чтобы судить об этом, поэтому я всегда просто принимал это на веру.Но это * действительно * проявляется во многих местах геометрии. Например, если вы рисуете пятиконечную звезду, отношение длины одной из двухточечных линий звезды к длине сторон пятиугольника внутри звезды будет φ: 1:
φ также относится к ряду Фибоначчи. Если вы не помните, ряд Фибоначчи — это набор чисел, где каждое число в ряду является суммой двух предыдущих: 1,1,2,3,5,8,13, … Если Fib ( n) — это * n * ое число в серии, вы можете вычислить его как:
История
———
Есть масса историй об истории φ.Большинство из них — полнейшая койка.
Многие истории скажут вам, что пирамиды Египта якобы построены на соотношении φ — нет. Они не. Многие люди будут пытаться указать соотношения греческих храмов, которые предположительно являются φ. Нет — это просто апофения, как у Гэри Осборна и его углов в 23,5 градуса.
Мы действительно знаем, что φ был идентифицирован кем-то из культа Пифагора — вполне возможно, Гиппасом, нашим бедным утонувшим другом из истории иррациональных чисел.
Это было хорошо известно древним грекам: Евклид пишет об этом в своих «Элементах»; и Платон писал об этом в своих философских трудах.Фактически, я бы сказал, что Платон является инициатором всей причудливой отрывистой метафизической тарабарщины, часто связанной с φ: он считал, что мир состоит из четырех элементов, каждый из которых образован из совершенных многогранников; допустимые многогранники были построены из треугольников, которые включали в себя некоторые предположительно совершенные отношения, в первую очередь отношение φ. Таким образом, для Платона φ была одной из самых фундаментальных частей Вселенной.
Причина, по которой он называется φ, на самом деле отсылка к греческому художнику, который использовал его в своих композициях; его имя (потеряно в моих записях) начиналось с буквы ф.
После греков к φ не проявляли особого интереса до XVI века, когда монах по имени Пачоли написал текст под названием «Божественная пропорция», в котором обсуждалось φ и его использование в архитектуре и искусстве. Да Винчи изучал текст Пачоли и был очарован φ, в конечном итоге он сыграл важную роль во многих из этих эскизов и картин. В частности, его печально известный набросок «Витрувианский человек» является иллюстрацией того, как человеческое тело якобы воплощает божественную пропорцию φ.
Конечно, как только да Винчи принял его, художники и архитекторы по всей Европе сразу же подхватили его, и он в значительной степени продолжает использоваться художниками и архитекторами вплоть до настоящего времени.
Необычное использование φ
————————
φ действительно удается появляться в некоторых удивительно странных местах. Основная гамма, используемая в западной музыке, построена на последовательности Фибоначчи, которая, как я сказал выше, глубоко связана с φ. Этим воспользовались несколько музыкантов; на самом деле Бела Барток использовал его как фундаментальную конструкцию в некоторых своих произведениях, особенно в прекрасной 12-частной фуге в своей «Музыке для струнных, перкуссии и Селесты».
На φ можно построить систему счисления, называемую φ-нари.Интересно то, что, несмотря на то, что φ является иррациональным числом, каждое целое число имеет * завершающее * представление в φ-нари; но каждая * дробь * имеет * неограниченное * представление в φ-нари. Φ-nary * полезен * для чего-нибудь? Не особо, но все равно довольно аккуратно!
.
 При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Но при этом мебель подбирается пропорциональной по высоте, а не по длине. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
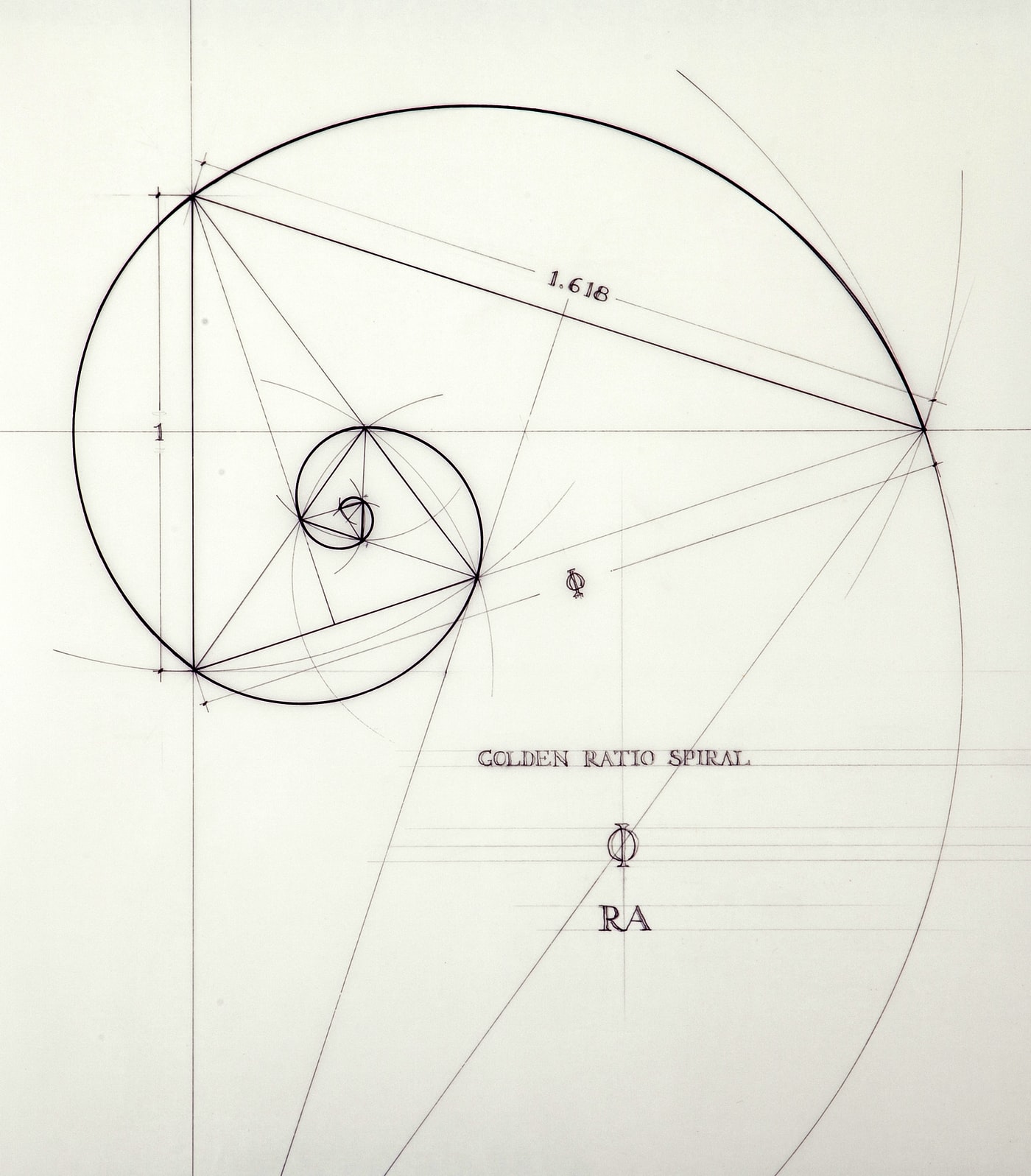

 В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.
В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.
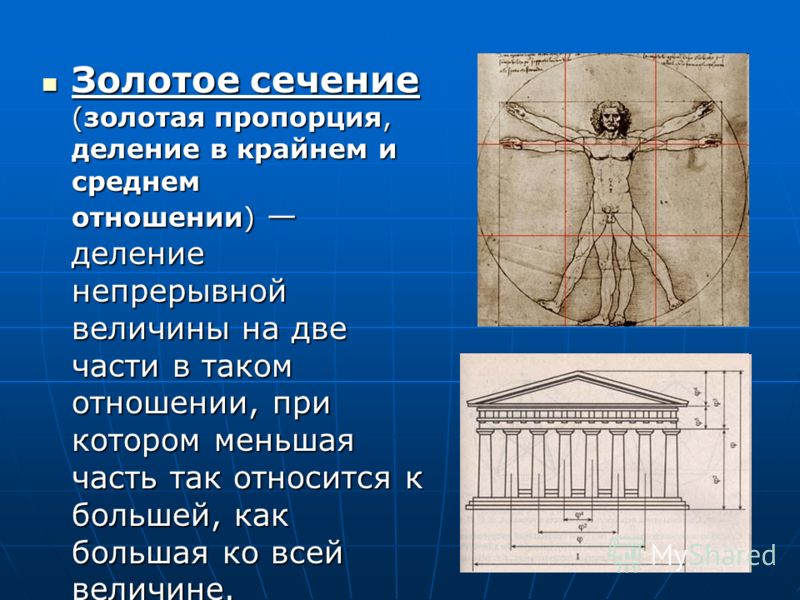 При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.