Декартово дерево: Часть 1. Описание, операции, применения / Хабр

Содержание

My tech notes — Декартово дерево

Такое волшебное дерево, которое хранит в каждой вершине по два параметра, и при этом по ключам является деревом поиска, а по приоритетам — кучей.

Поля у составляют дерево приоритетов, а поля х могут браться либо случайно из диапазона или на основании любых достаточно случайных пользовательских данных. От их случайности зависит насколько высоким будет дерево. При хорошем рандоме полученное декартово дерево с очень высокой, стремящейся к 100% вероятностью, будет иметь высоту, не превосходящую 4 log2 N.

Вся подноготная работы с декартовым деревом заключается в двух основных операциях: Merge и Split

Merge

Операция Merge принимает на вход два декартовых дерева L и R. От нее требуется слить их в одно, тоже корректное, декартово дерево T. Следует заметить, что работать операция Merge может не с любыми парами деревьев, а только с теми, у которых все ключи одного дерева ( L ) не превышают ключей второго ( R )

Алгоритм работы Merge очень прост. Какой элемент станет корнем будущего дерева? Очевидно, с наибольшим приоритетом. Кандидатов на максимальный приоритет у нас два — только корни двух исходных деревьев. Сравним их приоритеты; пускай для однозначности приоритет y левого корня больше, а ключ в нем равен x. Новый корень определен, теперь стоит подумать, какие же элементы окажутся в его правом поддереве, а какие — в левом.

Легко понять, что все дерево R окажется в правом поддереве нового корня, ведь ключи-то у него больше x по условию. Точно так же левое поддерево старого корня L.Left имеет все ключи, меньшие x, и должно остаться левым поддеревом, а правое поддерево L.Right… а вот правое должно по тем же соображениям оказаться справа, однако неясно, куда тогда ставить его элементы, а куда элементы дерева R?

Стоп, почему неясно? У нас есть два дерева, ключи в одном меньше ключей в другом, и нам нужно их как-то объединить и полученный результат привесить к новому корню как правое поддерево. Просто рекурсивно вызываем Merge для L. Right и дерева R, и возвращенное ею дерево используем как новое правое поддерево. Результат налицо.

Симметричный случай — когда приоритет в корне дерева R выше — разбирается аналогично. И, конечно, надо не забыть про основу рекурсии, которая в нашем случае наступает, если какое-то из деревьев L и R, или сразу оба, являются пустыми.

Теперь об операции Split. На вход ей поступает корректное декартово дерево T и некий ключ x0. Задача о1перации — разделить дерево на два так, чтобы в одном из них ( L ) оказались все элементы исходного дерева с ключами, меньшими x0, а в другом ( R ) — с большими. Никаких особых ограничений на дерево не накладывается.

Рассуждаем похожим образом. Где окажется корень дерева T? Если его ключ меньше x0, то в L, иначе в R. Опять-таки, предположим для однозначности, что ключ корня оказался меньше x0.

Тогда можно сразу сказать, что все элементы левого поддерева T также окажутся в L — их ключи ведь тоже все будут меньше x0. Более того, корень T будет и корнем L, поскольку его приоритет наибольший во всем дереве. Левое поддерево корня полностью сохранится без изменений, а вот правое уменьшится — из него придется убрать элементы с ключами, большими x0, и вынести в дерево R. А остаток ключей сохранить как новое правое поддерево L. Снова видим идентичную задачу, снова напрашивается рекурсия!

Возьмем правое поддерево и рекурсивно разрежем его по тому же ключу x0 на два дерева L’ и R’. После чего становится ясно, что L’ станет новым правым поддеревом дерева L, а R’ и есть непосредственно дерево R — оно состоит из тех и только тех элементов, которые больше x0.

Симметричный случай, при котором ключ корня больше, чем x0, тоже совершенно идентичен. Основа рекурсии здесь — случаи, когда какое-то из поддеревьев пустое.

Добавление элемента.

Помня универсальность операций Split/Merge, решение напрашивается практически сразу:

Разделим (split) дерево по ключу x на дерево L, с ключами меньше икса, и дерево R, с большими.
Создадим из данного ключа дерево M из единственной вершины (x, y), где y — только что сгенерированный случайный приоритет.

Объединим (merge) по очереди L с M, то что получилось — с R.

У нас тут 1 применение Split, и 2 применения Merge — общее время работы O(log2 N). Короткий исходный код прилагается.

Удаление элемента

1. Разделим сначала дерево по ключу x-1. Все элементы, меньшие либо равные x-1, отправились в левый результат, значит, искомый элемент — в правом.

2. Разделим правый результат по ключу x (здесь стоит быть аккуратным с равенством!). В новый правый результат отправились все элементы с ключами, большими x, а в «средний» (левый от правого) — все меньшие либо равные x. Но поскольку строго меньшие после первого шага все были отсеяны, то среднее дерево и есть искомый элемент.

3. Теперь просто объединим снова левое дерево с правым, без среднего, и дерамида осталась без ключей x.

Время работы операции все так же O(log2 N), поскольку мы применили 2 раза Split и 1 раз Merge.

https://habrahabr.ru/post/101818/

книги — Python, декартово дерево поиска

Добрый день!

Я новичок и пытаюсь сейчас реализировать декартово дерево поиска на python. Нужно написать несколько реализаций: — RandomTreap: использование рандомных переменных в качестве приоритетов — DynamicTreap: когда при каждом обращении к элементу его приоритет повышается и дерево переструктурируется, таким образом элементы с наибольшей частотой обращения передвигаются наверх. При первом внедрении элемента его приоритет равен 1.

Идеи: У меня уже есть реализация бинарного дерева поиска на питоне, имею представление, как написать функции поворота дерева. Опираясь на реализацию бинарного дерева, можно ее видоизменить, добавив атрибут priority. И изменить функцию insert: если ключа еще нет в дереве, то он добавляется как, как в бинарном дереве, а потом дерево поворачивается. Если ключ есть, то в RandomTreap ничего не происходит, а в DynamicTreap приоритет увеличивается на 1 и дерево поворачивается.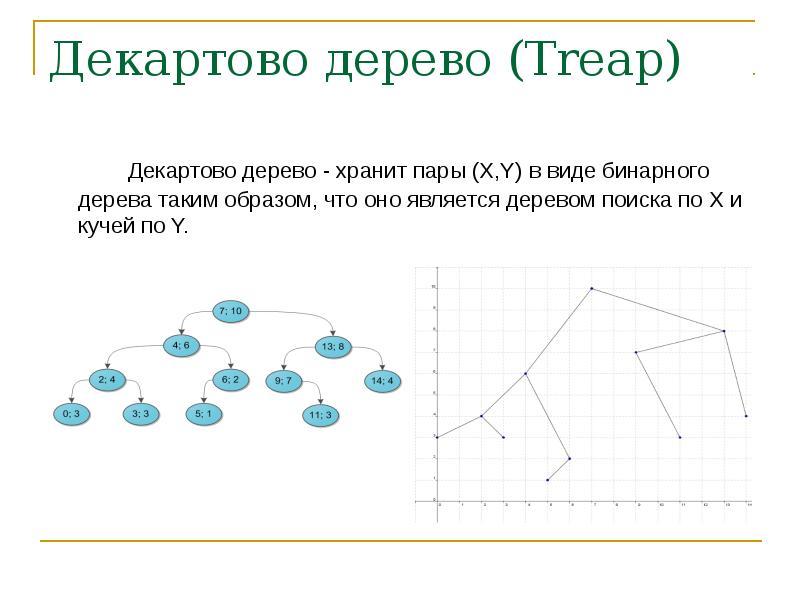

Просьба: Мне пока сложно написать все это сразу, поэтому предварительно хотелось бы почитать хорошие описания/ частичную реализацию на питоне, чтобы во всем хорошенько разобраться. Увы, похоже, что из-за скорости декартовы деревья поиска обычно не пишут на пионе, и я не могу найти в интренете почти ничего хорошего. Может быть, кто-то может посоветовать хорошие ссылки?

Заранее огромное спасибо!!!

python
книги
дерево
бинарное-дерево

Ознакомиться с созданием различных куч и деревьев можно по книге Problem Solving with Algorithms and Data Structures, рабочая ссылка на перевод: http://aliev.me/runestone/index.html

Про декартовы деревья хорошая статья, где описана реализация методов: http://opentrains.mipt.ru/zksh/files/zksh3015/lectures/zksh_cartesian.pdf.

Надеюсь я вам хоть немного помог.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

By clicking “Отправить ответ”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.

cartesian-tree — Реализация Rust // Lib.rs

Преобразование любого массива в декартово дерево в линейном времени.

Фон

Декартово дерево является производной структурой данных. Он получен из базового массива. Более формально декартово дерево T массива A представляет собой минимальную двоичную кучу элементов A . организованы таким образом, что обход дерева по порядку дает исходный массив.

Чтобы построить декартово дерево из базового массива, мы руководствуемся следующим:

Обход по порядку должен давать элементы массива в их
Дерево должно быть минимальной кучей. То есть самый маленький элемент должен быть в корне.
При обходе по порядку правый дочерний элемент извлекается после родительского и левого дочерних элементов — следовательно, самый правый узел будет последним извлеченным узлом.

Подождите, но почему?

Почему важны декартовы деревья? Они весьма полезны при решении Range Min Query 9.Проблема 0008: имея декартово дерево для массива, мы можем ответить на любой RMQ для этого массива. В частности, $RMQ_A(o, j) = LCA_T(A[i], A[j])$. То есть мы можем ответить на RMQ, выполнив поиск низших общих предков в декартовом дереве. Подробнее см. здесь.

`Детали реализации`

Мы строим декартово дерево постепенно, добавляя элементы в том порядке, в котором они появляются в массиве. Чтобы добавить элемент X , мы проверяем правый стержень дерева, начиная с самого правого узла. Мы следуем родительским указателям, пока не найдем элемент,

 Y  , в дереве меньше  X  . Мы модифицируем дерево, сделав  X  правым потомком  Y  . Мы также делаем остальную часть правого поддерева ниже  X  левым поддеревом нового узла.
 Обход правого стержня дерева от самого правого узла может быть выполнен эффективно, если хранить узлы на правом стержне в стеке. Таким образом, самый правый узел всегда находится на вершине стека.
 Изоморфизмы декартовых деревьев 
 Когда два декартовых дерева для двух разных массивов  A  и  B  имеют одинаковую форму? Как мы можем сказать это эффективно?
 Проще говоря, если два массива имеют одинаковую форму декартова дерева, то минимальные значения в  любом диапазоне  в обоих массивах встречаются с одним и тем же индексом. Это означает, что последовательность операций 
  Push  и  Pop  при построении декартовых деревьев для двух массивов абсолютно одинакова. Следовательно, чтобы узнать, изоморфны ли два массива, мы могли бы просто сравнить операции, необходимые для построения каждого дерева.
 Кстати, когда нас интересует только наличие двух массивов изоморфных деревьев, нам даже не нужно строить дерево. Вместо этого мы можем создать битовую строку из последовательности операций  Push  и  Pop . Число, образованное этой битовой строкой, называется числом декартова дерева   . Следовательно, в этой схеме   два массива имеют изоморфные деревья, если они имеют одинаковый номер декартова дерева.  
 Дополнительная литература 
 Декартовы деревья, примененные к задаче RMQ
 DROPS — сопоставление подпоследовательностей декартовых деревьев  Schloss Dagstuhl - Leibniz-Zentrum für Informatik GmbH
Schloss Dagstuhl - Leibniz-Zentrum für Informatik GmbH
научная статья
en
Оидзуми, Цубаса; Кай, Такеши; Миено, Такуя; Инэнага, Сюнсуке; Аримура, Хироки
https://www.dagstuhl.de/lipics
Лицензия: Лицензия Creative Commons Attribution 4.0 (CC BY 4.0) 
  . При цитировании этого документа используйте следующий 
 DOI:  10.4230/LIPIcs.CPM.2022.14  
 URN:  urn:nbn:de:0030-drops-161414  
 URL:  https://drops.dagstuhl.de/opus/volltexte/2022/161 41/
  Оидзуми, Цубаса  ;  Кай, Такеши  ;  Миено, Такуя  ;  Иненага, Сюнсуке  ;  Аримура, Хироки  Сопоставление подпоследовательности декартова дерева 
 pdf-формат: 
 Аннотация 
 Парк и др. [TCS 2020] заметил, что сходство между двумя (числовыми) строками можно зафиксировать с помощью декартовых деревьев: Декартово дерево строки — это двоичное дерево, рекурсивно построенное путем выбора наименьшего значения строки в качестве корня дерева. Говорят, что две строки одинаковой длины соответствуют декартовым деревьям, если их декартовы деревья изоморфны. Парк и др. [TCS 2020] представила следующую задачу сопоставления подстрок декартова дерева (CTMStr): по заданной текстовой строке T длины n и строке шаблона длины m найти каждую последовательную подстроку S = T[i..j] текстовой строки T. такое, что декартово дерево S и P совпадает. Они показали, как решить эту задачу за время Х(n+m). В этой статье мы вводим проблему сопоставления подпоследовательностей декартова дерева (CTMSeq), которая требует найти каждую минимальную подстроку S = T[i..j] строки T такую, что S содержит подпоследовательность S', декартово дерево которой соответствует P. Мы доказать, что проблема CTMSeq может быть решена эффективно за время O(m n p(n)), где p(n) обозначает время обновления/запроса для динамических предшествующих запросов.
   Используя подходящую структуру данных динамического предшественника, мы получаем O(mn log log n) решение для CTMSeq во времени и O(n log m) в пространстве. Это контрастирует с CTMSeq с близкородственным сопоставлением подпоследовательностей с сохранением порядка (OPMSeq), которое, как было показано Bose et al., является NP-жестким. [ИПЛ 1998].
 BibTeX - Вход 
  @InProceedings{oizumi_et_al:LIPIcs.CPM.2022.14,
 автор = {Оидзуми, Цубаса и Кай, Такеши и Миено, Такуя и Инэнага, Шунсуке и Аримура, Хироки},
 title = {{Сопоставление подпоследовательности декартова дерева}},
 booktitle = {33-й ежегодный симпозиум по комбинаторному сопоставлению шаблонов (CPM 2022)},
 страницы = {14:1--14:18},
 серия = {Международные труды Лейбница по информатике (LIPIcs)},
 ISBN = {978-3-95977-234-1},
 ISSN = {1868-8969},
 год = {2022},
 объем = {223},
 редактор = {Баннай, Хидео и Голуб, Ян},
 издатель = {Schloss Dagstuhl -- Leibniz-Zentrum f{\"u}r Informatik},
 адрес = {Дагштуль, Германия},
 URL = {https://drops.