Цифра объемная из бумаги: Цифра на день рождения своими руками. Как сделать плоские и объемные цифры для мальчика, девочки. Пошаговые мастер-классы

Содержание

Мастер-класс смотреть онлайн: Делаем большую цифру из картона и бумаги

Для дочки на 2 годика я делала две цифры. День рождения мы украшали в стиле маленькой принцессы. Все было в нежных розовых и белых тонах. Так же и цифры. Одна — большая, изготавливалась для фотосессии. Вторая — маленькая, для украшения стола. В этом мастер классе я покажу, как делала большую цифру.

Что понадобилось:

— картон белый;

— блестящая краска;

— пенопласт;

— гофрированная бумага;

— горячий клей;

— двусторонний скотч;

— шпажки;

— зубочистки;

— бусины на леске;

— пух марабу.

Процесс:

Для начала вырезаем из пенопласта основу цифры. Так как пенопласт толщиной всего 5 см, а цифра большая, пришлось вырезать 2 основания и склеить их между собой. С пенопластом мне работать гораздо легче, чем с картоном, поэтому я выбрала именно этот материал.

Затем делаем заготовки из бумаги.

Бумага использовалась флористическая (Италия).

После чего скручиваем розочки. Я советую сначала сделать заготовки цветов, а затем уже клеить их на основу. Потому что если делать один цветок и сразу клеить его, то уйдет гораздо больше времени.

Сам процесс несложный! На основу наклеиваем готовые цветы. После чего клеим бумагу по краям, чтобы закрыть пенопласт. Все это клеим на двусторонний скотч. Он хорошо держит цветы на пенопласте. Зубочистки вставляем внутрь цветов. Не обязательно, но желательно, так как они не будут заваливаться.

Затем клеим на горячий клей пух и корону. Корону делаем на белом картоне. Просто рисуем нужную форму, прокрашиваем золотой краской и вырезаем. Шпажки устанавливаем снизу как ножки для устойчивости.

Бусины (на леске) просто вставляем между цветов. Клеить их не обязательно.

Всего было изготовлено 305 розочек. Высота цифры около 80 см. Леска с бусинами — 5 метров.

К сожалению, фото подробных у меня не осталось, поэтому прилагаю подробное видео мастер-класса.

Как сделать цифру из бумаги своими руками: идеи красивого праздничного аксессуара

Любой праздник для человека это море эмоций, веселье целый день, повод провести время в компании друзей и близких и, как следствие, фотографии – приятные воспоминания. В такой день хочется всего особенного, в том числе и торжественную обстановку. А гораздо приятнее украшать место проведения аксессуарами, изготовленными собственноручно. Да, несомненно, поисковые системы заполнены услугами агентств по украшениям зала, дизайнеров и прочими специалистами в этой сфере.

Но, ваше время и наша статья поможет вам сэкономить средства на оплату таких услуг и дать волю фантазии. Все больше оборотов набирает оформление праздника фигурами из шаров и цифрами из бумаги. Именно о последнем способе эта статья. Мы подробно расскажем вам о каждом из вариантов (а их достаточно, чтоб выбрать тот, который вам приглянулся) как изготовить цифру для дня рождения, юбилея, дружеской вечеринки или для встречи выпускников, из бумаги, с минимум затрат и конечно же своими руками. Следуя советам в данной статье изготовление такого аксессуара станет увлекательным занятием и возможно вашим хобби и дополнительным доходом в будущем.

Итак, с чего-же начать

Самое главное — это желание. Вот вы уже в почти праздничном настроении, приятные хлопоты: приготовление стола, выбор нарядов и конечно же украшение помещения, чтобы это ни было: ваша квартира, торжественный зал, ресторан или даже ваш загородный дом — все должно соответствовать праздничному событию и вашему настроению. Несомненно на вашем празднике будет фотограф, и для эффектной фотосессии просто необходим красивый декор, но если уже потрачено много денег на закупку продуктов, приглашения, подарки и наряды — не стоит отчаиваться, вас спасут ваши руки и немного терпения.

Вы сами можете сделать отличный аксессуар для вашего торжества, большую цифру из гофрированной бумаги, и, поверьте, смотреться она будет не только на дне рождении. Идеальным вариантом, — применить такую цифру для фото сессии ко дню рождения вашего маленького чуда, конечно же, памятные фото с большой цифрой прекрасно впишутся в семейное портфолио.

Для более интересной задумки, делайте цифру каждый год размером соответственно росту вашего малыша, в годик он может стоять рядом, обняв цифру, в два года, например, может лечь возле нее в красивых подушках вышитых празднично, а вот в три года сможет уверенно поднять цифру над головой, якобы демонстрируя свои успехи в росте.

Такая цифра будет прекрасно подчеркивать годы, проведенные вместе, на юбилее свадьбы ваших родителей, на вечеринке по поводу дня рождения компании, в которой вы работаете, оформив такую цифру по особенному вы сделаете незабываемым вечер встречи выпускников и многие другие мероприятия.

Подготовка к выполнению работы

Вижу как вы уже настроились к плодотворной работе, горите желанием увидеть результат вашего труда, и давайте все-таки начнем. Для работы, в первую очередь вам нужно немного места, чтоб никто не мешал, идеально, если это будет стол, чтоб не сидеть на полу в неудобной позе и думать что это слишком сложно.

Проследите за тем, чтоб в помещении, где вы будете работать, было тепло, не жарко и не холодно, средняя температура, будет способствовать быстрому высыханию клея.

Для начала нужно приготовить необходимое количество материала. Вам понадобится картон (это может быть обычная магазинная коробка).

Мамочки могут использовать коробки из-под игрушек, наверняка где-то лежит пара от треков или от мобиля.

В зависимости от того, какой вы видите свою цифру: она может быть плоской, висеть на стене в окружении фотографий, или шаров. Как вариант, это может быть плоская двухстороння цифра, небольшого размера, украшена гофрированной бумагой и подвешена на шарики, наполненные гелием.

Для такого вида цифры вам понадобится немного картона, и немного материала для декора. В случае, если вам больше нравится объемная цифра, преимуществ ее тоже много, вам нужн

Как сделать цифры из салфеток своими руками

Сделать красочные цифры из картона и салфеток своими руками для важного события или даты: дня рождения, юбилея, годовщины, может каждый. Это должны быть объемные цифры из картона, декорированные цветами из салфеток? Фотосессия на фоне этих фигур будет незабываемой! Если всё сходится, начнем?

В сторону неуверенность и опасения, что получится не так красиво, как если бы Вы заказали их профессионалу! Наш мастер-класс поможет Вам шаг за шагом в этом увлекательном занятии. Итак, нам понадобятся:

картон;
карандаш;
ножницы/канцелярский нож;
малярный скотч;
клей;
салфетки;
степлер со скобами.

Такую красоту можно сделать своими руками!

Сколько надо салфеток

Покупаем самые простые салфетки. Первый вопрос, который возникает, сколько их понадобится? Всё зависит от того, какого размера цифру Вы будете делать.

Расход салфеток зависит от величины изготавливаемого цветка, плотности рядов, т.е. пышности фигуры. Можете сделать пробник из имеющихся дома салфеток, рассчитать площадь которую нужно задекорировать, и примерно прикинуть расход.

Если в планах сделать огромную цифру или две, то лучше закупиться оптом. Даже если останется, все равно потратите меньше, чем покупали бы поштучно.

По цветовой гамме определиться просто, например:

любимый цвет Ваш или виновника торжества;
основной тон интерьера;
розовые тона для девочки, синие для мальчика.

Они могут быть однотонными, разноцветными. Выбирайте сочетающиеся между собой оттенки!

Пример цветов цифр из салфеток для мальчика и девочки.

Основа цифры

На первом этапе делаем основу цифры. Подойдет любая картонная коробка, например, упаковка от бытовой техники. Если дома ничего не нашлось, можно купить картонные коробки в строительном гипермаркете, или гофрокартон в рулонах на отрез. Плотность выбирайте исходя из размера будущей цифры.

Размер фигуры зависит от намерений ее использования: если она будет украшением стола, конечно, она небольшого размера, нежели чем для фотосессии.

Общие инструкции для всех цифр

Так как фигура у нас объемная, нужно вырезать 2 одинаковые цифры и соединить их торцевыми частями. Для вырезания цифр можно использовать разные шаблоны и трафареты (ниже будут для каждой цифры предоставлены файлы для скачивания). Или нарисуйте сами на картоне нужную Вам цифру, вырежьте и используйте ее как трафарет для изготовления второй.

Дно

Нижнюю часть (примерно 20 см) основы делайте ровной, это будет дно, чтобы готовая фигура могла стоять.

Торцы

Боковины фигуры – прямоугольники одинаковой ширины лучше делать из слоеного картона, чтобы они хорошо ложились на изогнутые части фигуры.

Для устойчивости нашей поделки лучше, чтобы ширина прямоугольников – боковых частей была не менее 10 см. Высоту прямоугольников определяем, измеряя стороны фигуры. Для удобства на вырезанных деталях можно написать размеры каждого отрезка.

Клей

Заготовки склеиваются (например, клеем «Момент» или ПВА, а также горячим пистолетом), малярным скотчем или бумагой и клеем, так к ним будет проще прикреплять декор.

На обычный скотч цветы из салфеток крепиться не будут!

Не обязательно приклеивать малярный скотч по всей поверхности, нарежьте его на полоски и приклеивайте каждую отдельно сначала к одной стороне фигуры, затем к другой. Когда все боковины приклеены к одной из заготовок, для прочности проклейте все внутренние швы скотчем или клеем.

Теперь сверху накладываем вторую заготовку и прикрепляем бока скотчем. Для прочности это можно сделать несколько раз, особенно стыки.

Изготовление каркаса

Итак, приступаем к выполнению каркаса цифр. Фигуры состоят из прямоугольников, кругов разных диаметров, полуовалов. Так как фигура у нас объемная отдельные элементы заканчиваются торцами. Торцы имеют форму квадрата.
Выполнение отдельных деталей для разных цифр имеет свои особенности, разберемся:

Цифра 1

Это самая популярная цифра! Празднование первого года жизни малыша самое долгожданное событие. Эта фигура состоит только из прямоугольников, однако деталей нужно больше, чем для других.

Шаблон цифры 1:

Начнем с правого бокового прямоугольника, делаем замеры от верха фигуры до основания (перекладины внизу цифры). Закрепляем скотчем. Измеряем левый отрезок прямоугольника от изогнутой части до перекладины.
Оформляем верхнюю часть перекладины, понадобится два прямоугольника.
Вырезаем прямоугольник для дна, скрепляем.
Закрываем торцы фигуры квадратами, их нужно 4.
Для дугообразной верхней части на внутренней стороне картона можно сделать неглубокие надрезы, чтобы картон стал более податливым.

Смотрите видео мастер-класс по изготовлению единички:

Цифра 2

В отличие от единички, у двойки плавные изгибы, поэтому картонную основу для цифры будет сделать немного сложнее.

Шаблоны цифры 2:

Для оформления полуовала цифры отрезаем длинную полосу, соединяем ее с верхним полуовалом фигуры, то же самое делаем с внутренним.
Для исполнения «хвостика», его проще сделать прямым, готовим прямоугольники для верхней части и для дна.
3 торцевыми квадратами завершаем изготовление фигуры.

Смотрите видео мастер-класс по изготовлению двоечки:

Цифра 3

Праздничная дата состоит из цифры 3? Потребуется еще больше усилий.

Шаблоны для цифры 3:

Для двух внешних полуовалов: верхнего (меньшего размера) и нижнего (большего размера) необходимо вырезать по две длинные прямоугольные полосы, так же для внешнего, измерив предварительно данные отрезки.
На нижнюю часть внешнего полуовала – дно приклеиваем прямоугольник и к 3 торцам фигуры – квадраты.

Смотрите мастер-класс, как сделать цифру 3:

Цифра 4

Четверка похожа на единицу. Начало изготовления фигуры как для единицы, т.е. с правой стороны основного прямоугольника.

Шаблон цифры 4:

Делаем заготовку для левой стороны косого отрезка. Вместе с перекладиной они могут иметь форму угла или оформляются с помощью квадратного торца.
Далее по меркам отрезаем прямоугольники для верхней и нижней частей перекладины.
Для формирования внутреннего угла готовим три отрезка соответствующих размеров.
Дно этой цифры желательно утяжелить, например, деревянным бруском для устойчивости. Брусок прикрепите к внутренней стороне дна заранее.

Смотрите видео, как сделать своими руками четверку:

Цифра 5

Для цифры 5 выберите шаблон с более прямыми линиями, чтобы легче было вырезать и соединять элементы.

Шаблоны для 5-ки:

Первым делом оформим верхнюю часть, отмерив нужную длину на картоне, вырезаем и крепим прямоугольники сверху и снизу.
Готовим 2 длинных прямоугольника для внешнего и внутреннего полуовалов. Дно – прямоугольник длиной 20 см оформляем на нижней части полуовала.
Осталось закрыть торцы, их будет 4.

Смотрите видео мастер-класс как сделать каркас цифры 5 из картона:

Цифра 6

Состоит из большого внешнего круга и малого внутреннего, а также 2 полуовалов: внешнего и внутреннего.

Шаблоны цифры 6:

Оформляем дно внизу большого круга. Замеряем длины отрезков полуовалов, отрезаем полосы нужной длины. Скрепляем скотчем. Аналогично делаем замеры внутреннего круга, отрезаем прямоугольник и соединяем детали. Квадратом закрываем торец верхнего полуовала.

Цифра 7

Самая простая в исполнении цифра! Но придется подумать, как поставить надежно эту цифру вертикально.

Шаблоны для цифры 7:

Прямоугольник шаблона цифры 7 лучше делать изогнутым и укрепить дно, опять же с помощью деревянных брусочков или сделать дно из нескольких слоев картона, склеенных между собой.
Далее вырезаем 1 торцевой квадрат, дно, два прямоугольника для верхнего элемента и два длинных прямоугольника для изогнутых частей.

Цифра 8

Наверное, чаще эта цифра используется для украшения помещений к празднованию женского дня.

Шаблоны для 8-ки:

Восьмёрка состоит из 2 кругов: большого и малого. Предварительно измерив их, готовим 2 длинных прямоугольника для двух внутренних кругов. Внешние круги можно соединять длинной прямоугольной полосой или собрать боковину цифры из нескольких коротких, склеивая их между собой.

Смотрите мастер-класс, как сделать цифру 8 из картона и салфеток:

Цифра 9

Девятка выполняется аналогично цифре 6. Помним, что дно у фигуры будет на нижнем полуовале, у шестерки на нижней окружности!

Шаблон 9-ки:

Цифра 0

Эта фигура «любит» круглые даты!

Трафарет для цифры 0:

Заготавливаем один большой овальный круг и две длинные прямоугольные полосы для изогнутых боковин: наружной и внутренней. Отмеряем 20 см внизу для дна.

Смотрите видео, как сделать цифру 0:

Декор цифры

Приступаем ко второму этапу. Декорировать полученную фигуру можно разными материалами и способами, всё зависит от Ваших предпочтений.

Мы будем украшать бутонами цветов из простых бумажных салфеток. Это могут быть гвоздики, хризантемы, розы или, например, помпоны. Техника их выполнения несложная, но займет некоторое время:

Гвоздика

1 способ

Цифры из салфеток своими руками: как сделать и украсить

Здравствуйте, дорогие читатели! Как известно, праздник должен быть прежде всего в душе. Но если к этому прибавляются добрые искренние пожелания и подарки, то это еще лучше. А уж декор помещения в честь празднества так и вовсе способен превратить традиционное торжество в нечто особенное. Одним из простых и несложных способов украсить дом являются цифры из салфеток.

Подобные цифры приносят не только ощущение праздника, но и позволяют почувствовать себя профессиональным декоратором. Хотя на самом деле с подобной циферкой при должном старании способен справиться даже начинающий. Приступим!

Необходимые материалы

Необходимые материалы я решила представить в виде списка:

Основа. Ей уделите особое внимание. Самым распространенным видом для ее создания являются картонные коробки и пенопласт. Коробки можно использовать как из-под крупной бытовой техники, так и небольшие – из-под сока и т.п. Чем больше желаемый размер цифры, тем больше коробка.
Салфетки. Пригодится несколько пачек. Можно использовать другие виды бумаги, например, гофрированную.
Клей или шпажки для крепления цветов и других украшений к основе.
Ножницы или канцелярский нож. Последний особенно актуален для разрезания пенопласта.
Двусторонний и бумажный скотч. Для пенопласта вам понадобится первый, а для картона – второй.

Цветы из салфеток: 5 вариантов для украшения цифр

Прежде чем приступить к созданию непосредственно цифр из картона, пенопласта и салфеток, нужно понять, как мы эти цифры будем украшать. Есть много вариантов создания главного декоративного элемента – цветов.

Первый и самый распространенный – вот такие пушистые розочки, которые легко можно сделать из салфеток. Для этого вам понадобится салфетка, сложенная в несколько раз, степлер, шаблон круга и ножницы.

Ход работы:

Сложите несколько салфеток так, чтобы из каждой получился квадрат. Чем больше слоев, тем пышнее будет цветок.
Приложите к получившейся стопке круг и вырежьте круги из всех слоев разом.
Скрепите цветок в центре степлером.
Каждый слой поднимите таким образом, чтобы получился пышный лепесток.

Можно сделать конструкции большего размера. Для этого возьмите салфетки и сложите их гармошкой в несколько слоев. Края обрежьте полукругом, центр перевяжите ниткой. Распушите края – цветок готов.

Подобным образом можно сделать и цветок ниже. Отличием будет являться только то, что края полукругом обрезать не надо. Такие дополнения для цифры можно сделать не только из бумажных салфеток, но и из разных видов бумаги – например креповой.

Для следующего цветка салфетку понадобится сложить в 4 раза. Нарисуйте на этой основе полукруг как показано ниже и обрежьте края. Понадобится несколько слоев.

Из гофрированной бумаги можно создать вот такие розы. Вариант не такой бюджетный, как с салфетками, но эффект получается весьма необычный.

Если вы хотите узнать о других возможных украшениях цифр цветами, то рекомендую посетить эту статью. Найдется цветок для любой задумки

Сколько салфеток и цветов понадобится?

Все зависит от размера готового изделия. Но приготовить стоит от 3 до 5 пачек салфеток. Цветов у вас уйдет, скорее всего, от 200 до 500 на штуку.

От чего зависит количество цветов:

от размера цветка и готовой цифры,
от пышности декоративного элемента,
от плотности рядов.

Другие способы украшения цифр

Кроме самого очевидного способа, рассмотренного выше, есть другие методы. Например, создание бахромы – это куда быстрее, чем создавать множество цветов и приклеивать их. Как сделать бахрому вы можете прочитать в статье про создание пиньяты. Там бумага складывается вдвое, благодаря чему создается впечатление объема. Но можно использовать однослойную бахрому – так уйдет меньше бумаги или салфеток.

Общий принцип работы такой: вырежьте полоску бумаги и нарежьте ее край. Не нарезанную часть приклейте к цифре. Каждый слой приклеивайте так, чтобы предыдущий перекрывал не нарезанную верхушку.

Помимо этого можно прибегнуть и к другим способам. Например, торцеванию, когда декоративные квадратные листочки бумаги центром прикрепляются к основе (в основном пенопластовой). А может быть вы решите создать что-то необычное – скажем, множество завитков в технике квиллинг на поверхности цифры.

Как сделать цифры из салфеток своими руками на День рождения и не только

Самой главной датой, на которую обычно приходится изготовление и оформление праздничных цифр, является День рождения и юбилей. Хотя в чести Новый год и другие памятные торжества. Однако как же справиться с созданием такого праздничного декора?

Общие рекомендации

Для всех изделий будет актуально:

Экономию времени даст обклеивание боковых сторон и дна бумагой или теми же салфетками. Тогда времени на украшение цифры уйдет гораздо меньше.
Цветы берите наиболее объемные, пышные, чтобы несколькими штуками легко можно было украсить большую поверхность сразу.
Отдайте предпочтение клею, который быстро схватывается и легко выдавливается из тары. Для легких салфеток также можно использовать двусторонний скотч (хотя это более затратный вариант).

Цифра 1

Самой популярной цифрой является 1. Это и неудивительно – обычно ее используют для оформления первого месяца и первого годика жизни малыша. Сделать основу для такого украшения можно из картонных коробок либо из пенопласта.

Для объемного картонного варианта нужно вырезать переднюю и заднюю части как на фото. То есть просто 2 плоских единицы. Боковые части состоят из прямоугольников одинаковой ширины, а высота их должна соответствовать высоте каждого отрезка единицы (опять же, смотрите на фото).

Цветочное оформление может быть абсолютно разным. Только вы выбираете тот вид украшения, который наиболее симпатичен для вас.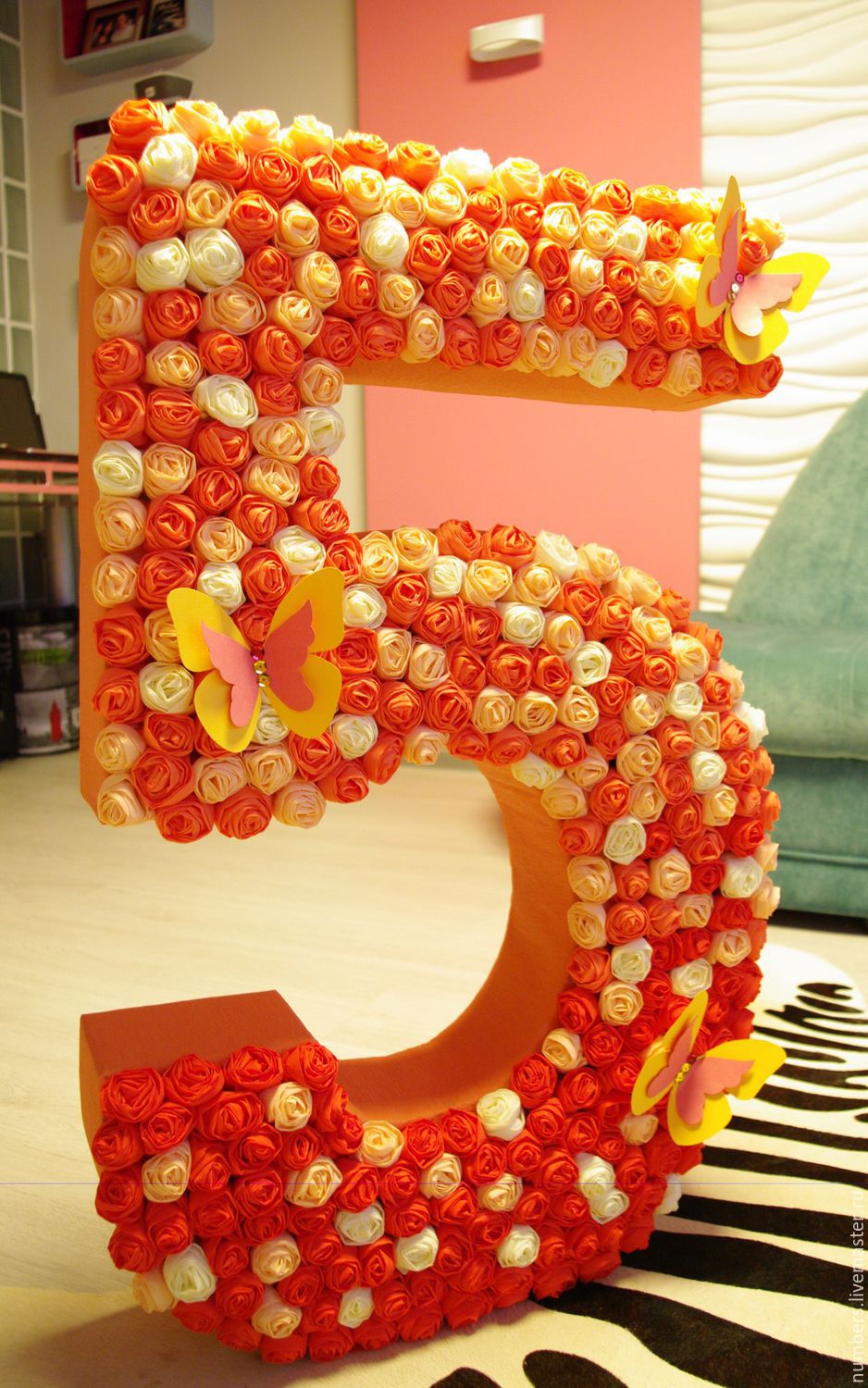

Единица в стиле Микки Мауса – дизайнерская вещица для костюмированной вечеринки.

Трехмерные фигуры — Космические фигуры

В пространство, в котором мы живем, имеет три измерения: длину, ширину и высоту. Трехмерный геометрия, или геометрия пространства, используется для описания зданий, в которых мы живем и работы, инструменты, с которыми мы работаем, и объекты, которые мы создаем.

Сначала мы посмотрите на некоторые типы многогранников. Многогранник — это трехмерная фигура гранями которого являются многоугольники. Его название происходит от греческого «поли». что означает «многие» и «хедра», что означает «лица».» Древние греки в 4 веке до н. Э. были блестящими геометрами. Oни сделали важные открытия и, как следствие, получили названия объектов они обнаружили. Вот почему геометрические фигуры обычно носят греческие названия!

Мы можем связать некоторые многогранники — а также другие космические фигуры — к двумерному цифры, с которыми мы уже знакомы. Например, если вы переместите вертикальный прямоугольник по горизонтали через пространство, вы создадите прямоугольный или квадратный призма.

Если вы переедете вертикальный треугольник по горизонтали, вы создаете треугольную призму. когда сделанная из стекла, призма этого типа разделяет солнечный свет на цвета Радуга.

А теперь давайте посмотрите на некоторые космические фигуры, которые не являются многогранниками, но также связаны к знакомым двумерным фигурам. Что можно сделать из круга? Если вы перемещаете центр круга по прямой, перпендикулярной круг, вы получите цилиндр.Вы знаете эту форму — цилиндры используются в качестве трубок, колонн, банок, музыкальных инструментов и во многих других областях.

Банка с конусом создается путем вращения прямоугольного треугольника вокруг одной из его ног. Это еще одна знакомая космическая фигура с множеством применений в реальном мире. Если вам нравится мороженое, вы наверняка знакомы хотя бы с одним из них!

Сфера создается, когда вы вращаете круг вокруг одного из его диаметров.Это один наших самых распространенных и знакомых форм — фактически, та самая планета, на которой мы живем это почти идеальный шар! Все точки сферы находятся в такое же расстояние от его центра.

Есть многие другие космические фигуры — по сути, бесконечное число. У некоторых есть имена и некоторые нет. Вы когда-нибудь слышали о «ромбикосододекаэдре»? Некоторые утверждают, что это одна из самых привлекательных трехмерных фигур с равносторонними треугольники, квадраты и правильные пятиугольники для его поверхностей.Геометрия мир в себе, и мы просто касаемся поверхности этого мира. В этом разделе мы остановимся на наиболее распространенных космических фигурах.

назад наверх

Трехмерные фигуры

Трехмерные фигуры Вернуться к содержанию

Обзор базовой геометрии — Урок 9

Обзор урока

Плоскости: параллельные, перпендикулярные и прочие

Точка, линия и плоскость — неопределенные термины.Несколько предположений были созданы вокруг них с помощью постулата «точка-линия-плоскость» в уроке 1. Для самолетов мы должны добавить еще три предположения ниже.

Плоскость Допущение: Если две точки лежат на плоскости, линия, содержащая их, лежит в плоскости.
Допущение уникальной плоскости: Через три неколлинеарных точки, есть ровно один самолет.
Пересекающиеся плоскости Допущение: Если две разные плоскости имеют общую точку, то их пересечение — линия.

Самолеты не имеют неровностей и, как линии, продолжаются вечно. Три (неколлинеарные) точки определяют плоскость. Также определяют три точки: треугольник; линия и точка не на линии; и две пересекающиеся линии. Ровно один самолет содержит их. Таким образом, стул на трех ножках стабилен, но большее количество ножек может вызвать стул качаться. Поскольку линии не имеют толщины, плоскости также не имеют толщины. Линия, не лежащая на плоскости, может пересекать плоскость не более чем в одной точке.

Мера наименьшего из всех возможных углов определяет угловая мера между линией и плоскостью.

Если линия l пересекает плоскость X в точке P , то линия l перпендикулярна плоскости X ( л X ) тогда и только тогда, когда l перпендикулярно каждой линии в X , которая содержит П .

Теорема о перпендикуляре прямой и плоскости: Если линия перпендикулярна двум разным линиям в их точке пересечения, то он перпендикулярен плоскости, содержащей эти прямые.

Две плоскости равны параллельным плоскостям тогда и только тогда, когда у них нет точек. общие или они идентичны. Опять же, это всеобъемлющее определение не используется повсеместно. Расстояние между параллельными плоскостями — это длина сегмента перпендикулярно плоскостям с конечной точкой в каждой плоскости.Расстояние между плоскостью и точкой не на ней измеряется. по перпендикулярному отрезку от точки к плоскости.

Когда две плоскости пересекаются, образуются четыре двугранных угла . Меру этих углов можно указать, построив лучей, перпендикулярных линии пересечения, и измеряя те углы образовались. Косые линии — это не компланарные линии, которые не пересекаются.

Так же, как есть разница между многоугольником и многоугольной областью, мы различаем поверхность трехмерной фигуры и пространство он включает.С этого мы начинаем твердотельную геометрию . Коробка , поверхность прямоугольного твердого тела , или параллелепипед — одна из самых важных трехмерных фигур. Коробка имеет шесть граней , каждая из которых представляет собой прямоугольную область. Противоположные грани лежат в параллельных плоскостях. Куб — это прямоугольник с квадратными областями всех граней. Края , — это линейные сегменты, где грани встречаются друг с другом. Конечными точками ребер являются вершин .Коробка имеет 12 ребер и 8 вершин. На рисунке справа показано типичное двумерное представление. а также tesserack или hypercube — это четырехмерный аналог куба. На рисунке слева показано двухмерное представление этого четырехмерного объекта. Подробнее об этом можно видел и найденный. Многие люди с трудом верят, что такое может существовать, поэтому такие книги, как Плоская земля (Эбботт, 1884 г.), Sphereland (Бюргерс, 1983), и Флаттерленд (Стюарт, 2001) были написано.

Цилиндрические твердые тела / поверхности: призмы и цилиндры

Цилиндрическое тело — это набор точек между областью и его переводное изображение в пространстве, включая регион и его изображение.

Цилиндрическая поверхность является границей цилиндрического твердого тела.
Цилиндр — это поверхность твердого цилиндрического тела с круглым основанием.
Призма — это поверхность цилиндрического твердого тела с многоугольным основанием.

Цилиндрические твердые тела имеют два основания , которые конгруэнтны и параллельны плоскостям. Поверхность без оснований известна как боковая поверхность . Высота или высота — это расстояние между плоскостями. баз. Если вектор трансляции перпендикулярен плоскостям основания, цилиндрическое тело — это правый цилиндр или правая призма , в противном случае это наклонный .Призмы названы по форме их основание. Неосновные грани призмы известны как боковые грани , которые сходятся на боковых краях . Правая призма, основание которой — правильный многоугольник это обычная призма .

Конические тела / поверхности: пирамиды и конусы

Коническое тело — это набор точек на любом сегменте между областью (основание ) и точка (вершина ) не в плоскости основание.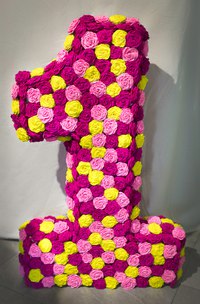

Коническая поверхность является границей конического твердого тела.
Пирамида — это поверхность конического твердого тела с многоугольным основанием.
Конус — это поверхность конического твердого тела с круглым основанием.

Конические тела имеют только одно основание . Пирамиды имеют боковых граней , которые соединяют вершины основания. многоугольник с вершиной . В конусе боковой кромкой является любой отрезок конечными точками которого являются вершина и точка на основной окружности.Треугольные, неосновные грани пирамиды — это боковых граней . Пирамиды и конусы также могут быть правыми или наклонными . Правая пирамида с правильным многоугольным основанием тоже правильная . Конус также имеет ось , которая является линия (не сегмент) через вершину и центр основания. высота коники — это расстояние между вершиной и вершиной. самолет, содержащий базу.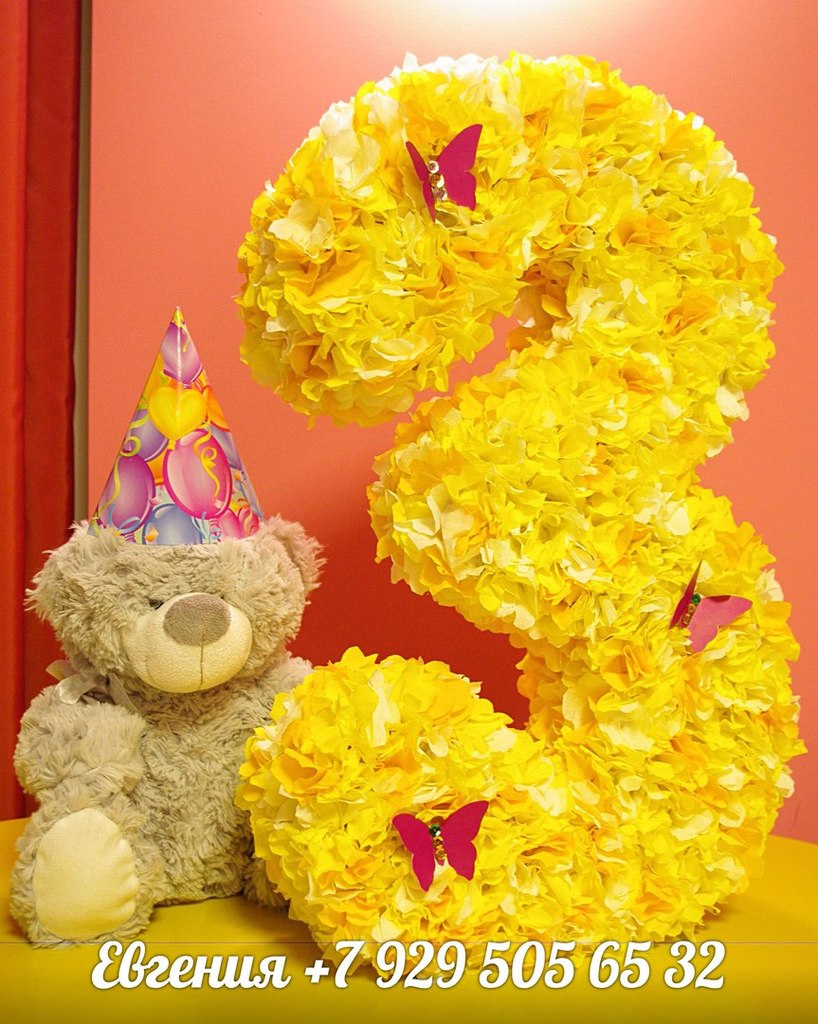 В правильной пирамиде наклонной высоты — высота любой боковой грани (треугольника).Только в правом конусе она равна длине бокового края. Конус или пирамида могут быть усеченными — многие стаканы усеченные конусы. Усеченный конус тоже известный как усеченная пирамида .

Сферы и прочие предметы круглые

Сфера — это набор точек в пространстве на определенное расстояние ( радиус ) от точки ( центр ).

Сферы имеют нулевых оснований .Сферу можно рассматривать как трехмерный аналог круга. Дважды радиус диаметра . Hypersphere или 4-ball — это четырехмерный аналог сферы. (Аналог намеренно пишется по-другому, но здесь тоже правильно.) Шар (круг, сфера, гиперсфера) размером n называется шаром n .

Плоское сечение трехмерной фигуры — это пересечение этой фигуры с плоскостью.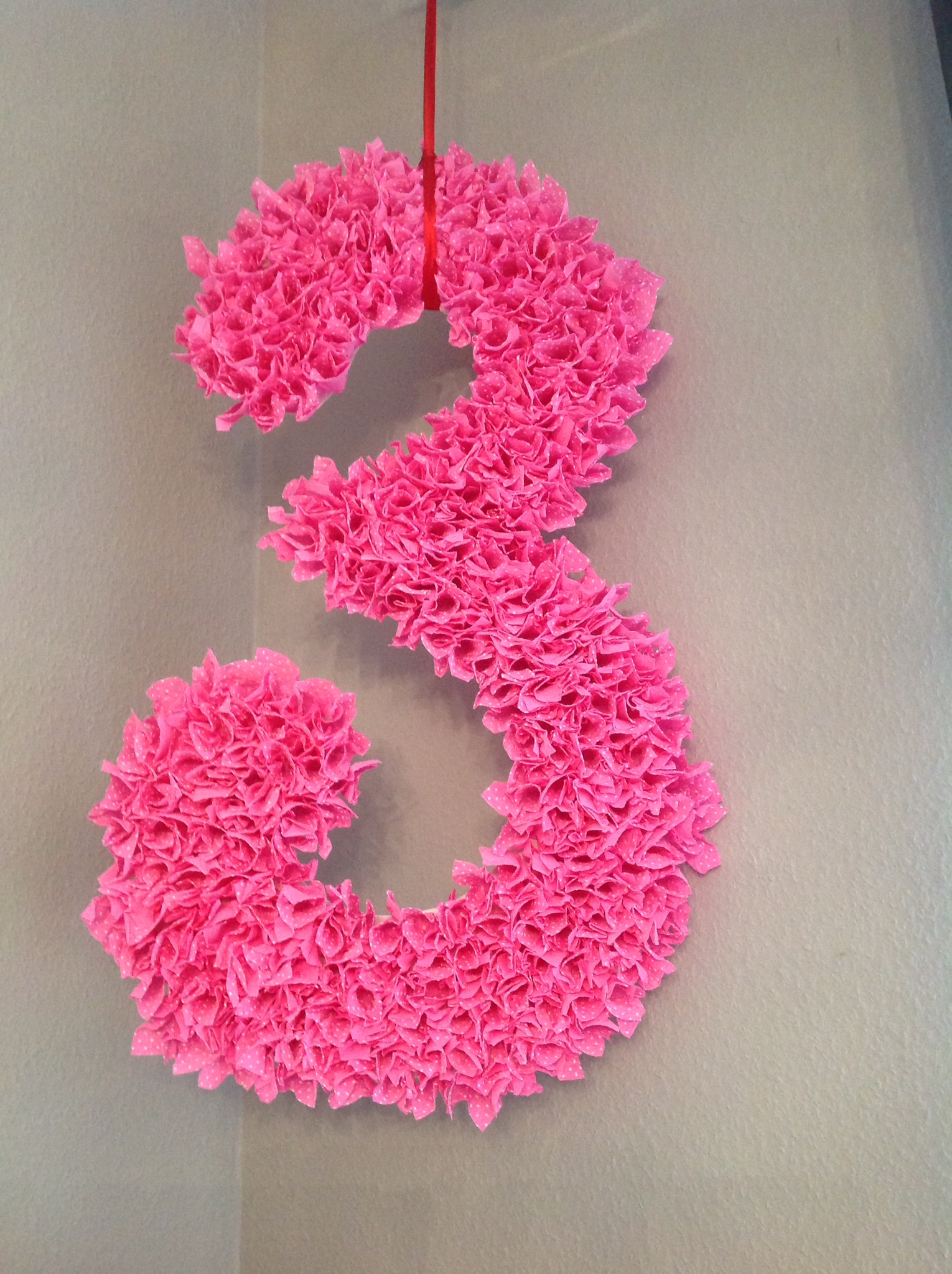

Сфера и плоскость могут пересекаться очень немногими способами. Во-первых, самолет мог касайтесь сферы только в точке. Эта плоскость должна быть касательной в этой точке. таким образом, линия, содержащая центр сферы и точку пересечение будет нормальным (перпендикулярным) к плоскости. Во-вторых, плоскость пересекается более чем в одной точке, и в этом случае пересечение это круг. Это пересечение называется маленьким кругом если плоскость не содержит центр круга, в этом случае он известен как большой круг .Большие круги делят сферы на полушарий , буквально полусферы. Маршруты большого круга очень важны в навигации, потому что они содержат кратчайшее расстояние между двумя точками на поверхности. Геодезическая — это общий термин для кратчайшего расстояния между двумя точками. Метрика — это термин из общей теории относительности. Так мы измеряем пространство-время. В терминах дифференциального исчисления это: dx ² + dy ² + dz ² — c ² dt ². Antipode с точностью до наоборот или наоборот; также точки сферы, такие как земля, которые диаметрально противоположны (противоположные концы диаметра).

Земля представляет собой сплюснутый сфероид (в форме M & M, то есть сплющенный на полюсах и из трех взаимно перпендикулярных радиусов повторяется тем длиннее). Вытянутый сфероид больше похож на футбольный мяч или сигару (из трех взаимно перпендикулярных радиусов повторяется тем короче).В эллипсоиде три взаимно перпендикулярных радиуса имеют разную длину. Посмотреть этот сайт для некоторых диаграмм и определений, включая тор или пончик.

Гипотеза Кеплера

К 1606 году Кеплер начал работу над тем, что стало известно как Гипотеза Кеплера после получения письма от Харриота которые работали над проблемой не менее 15 лет. Сэр Уолтер Рэли фактически предложил это своему помощнику Харриоту.Проблема заключается в наиболее эффективной упаковке для пушечных ядер или, в конечном счете, атомов в кристалле, хотя в то время об атомной структуре было известно немного.

В конце концов Кеплер предположил, что гранецентрированная кубическая (FCC) [и эквивалентно гексагональная плотная упаковка (HCP)] оба дали оптимальную плотность упаковки сфер. В конечном итоге эта проблема стала частью C проблемы 18 Гильберта. Знаменитый список из 23, созданный в 1900 году. До 1990-х годов это оставалось одним из последних нерешенные проблемы дискретной геометрии.В 1990 г. У-И Сян разослал препринты, а в 1992 г. представил для публикации 100-страничное доказательство, которое осталось неприемлемым в математическом сообществе из-за его нечеткость и отсутствие логической прогрессии. Хотя он был опубликован в International Journal of Mathematics , у некоторых есть «сомнения в серьезности процесса судейства» поскольку « Journal редактируется коллегами Сяна из Беркли». Это «нельзя считать доказательством».» ( Гипотеза Кеплера , Джордж Спиро, 2003, стр. 150.) Примерно в 1996 году Хейлз начал противоречивое доказательство, которое следует вычислительный подход. 9 августа 1998 г. Сэм Хейлз объявил доступность статей и препринтов, доказывающих гипотезу Кеплера. В январе 1999 г. недельный семинар, посвященный исключительно гипотезе Кеплера. прошел в Институте перспективных исследований в Принстоне, где эксперты чистил его со всех сторон. Они требовали публикации в Анналы математики .В конечном итоге он был (будет?) Опубликован, но с беспрецедентным отказом от ответственности, что судьи не могут проверить доказательство.

Конические секции

Nappes является множественным числом от Nappe . Конус называется двойным, если мы говорим о полном конусе. который больше похож на песочные часы или две «пирамиды с круговой основой» соединились в их вершинах. Одиночная «пирамида с круговым основанием» — это то, что большинство студентов подумают как конус.

Выше показано пересечение плоскости с конусом — двойным ворсанный конус. Эти локусов и (наборы точек) представляют собой конические секции. Loci имеет множественное число для , locus (набор точек). Эти конические сечения ( круг , эллипс , парабола , и гипербола ) будут изучены более подробно в алгебре II. См. Эту веб-страницу для получения дополнительной информации.

Платоновы тела

Платоново тело представляет собой выпуклые многогранники с все грани одинаковые многоугольники.
Как показано ниже, их ровно пять.

Платоновы тела также известны как правильные многогранники. Тетраэдр также известен как треугольная пирамида . Шестигранник также известен как куб . Двойники особенно важны в кристаллографии, где рассеянное излучение (электроны, нейтроны, рентгеновские лучи) лучше всего изучать в обратном пространстве. Глядя на приведенную выше таблицу, подумайте о формуле Эйлера который связывает количество граней, вершин и ребер любых многогранников: F + V = E + 2.

Нетрудно показать, что правильных многогранников всего пять. (выпуклый и грани все же правильный многоугольник). Подумайте, сколько одинаковых правильных многоугольников может сойтись в одной вершине. Нам всегда нужно больше двух, если мы собираемся сложить его и оградить любое пространство. Для треугольников (с углом 60 °) шесть составят мозаику плоскости. Следовательно, необходимо учитывать три, четыре и пять, и результаты могут быть рассматриваемый выше как тетраэдр, октаэдр и икосаэдр.Для квадратов (с углом 90 °) четыре будут мозаикой плоскости. Следовательно, нужно рассматривать только три, и куб является результатом. Для пятиугольника (с углом 108 °) четыре превышает 360 °. Следовательно, нужно рассматривать только три, и додекаэдр является результатом. Три шестиугольника (с углом 120 °) образуют мозаику на плоскости. Таким образом, мы исчерпали все возможности, в результате чего получилось пять правильные многогранники или платоновы тела.

Эта ссылка ведет на страницу с описанием пяти платоновых тел, цветные фигурки.Этот сайт есть твердые тела, которые можно вращать. Этот сайт ссылки на многие другие хорошие сайты. Древние связывали пять платоновых тел с огнем (4), землей (6), воздух (8), вода (20) и космос (12).

Твердые тела Архимеда

В Archimedian Solid твердое тело выпуклое, все вершины идентичны,
все грани — правильные многоугольники, но не все одинаковые.

Твердые тела Архимеда можно классифицировать по набору чисел, который указывает количество сторон многоугольников в каждой вершине.Таким образом, {3,6,6} будет обозначать один треугольник и два шестиугольника в каждой вершине. Остальные двенадцать: {3,8,8}; {4,6,6}; {3,10,10}; {5,6,6}; {3,3,4,4}; {3,3,5,5}; {3,4,4,4}; {4,6,8}; {3,4,4,5}; {4,6,10}; {3,3,3,3,4}; и {3,3,3,3,5}. Эта (неработающая) ссылка ведет на страницу с описанием тринадцати архимедовых или полурегулярных тел, в комплекте с цветными фигурами.

C ₆₀ — высокосимметричная молекула чистого углерода. Форма такая же, как у футбольного мяча или Archimedian Solid усеченный икосаэдр: {5,6,6}.C ₆₀ часто обозначается как Buckyballs. Технически это твердое тело Архимеда представляет собой усеченный изокаэдр г. Это имя происходит от имени Ричарда Бакминстера Фуллера, известен своими геодезическими куполами. Степан центр Нотр-Дам является местным примером. C ₆₀ является одним из класса известных соединений как фуллерены также называют в честь американского архитектора выше. Молекула C ₆₀ была открыта в 1985 году, когда группа пытался понять спектры поглощения межзвездной пыли.Их работа принесла им Нобелевскую премию по химии 1996 года. Первоначально производимый в очень малых количествах или извлекаемый из сажи, он теперь доступен и является центром множества разнообразных исследований. Длинные углеродные трубки называются нанотрубки также были произведены. C ₆₀ представляет собой новую, неожиданную кристаллическую форму твердого углерод. Другие формы: тетраэдрическая углеродная связь в алмазе. и соединение листового типа в графите имеет гораздо более долгую историю.Увидеть На этой странице представлена краткая, хорошо задокументированная история C ₆₀.

Пентамино

Пентамино.

Мои исследовательские интересы связаны с утроением пентамино из подмножество 9 из 12. Сможете ли вы утроить все 9 в наборе или даже все 12? Можете ли вы втрое повторить данное пентамино со всеми 220 подмножествами?

Симметрия, виды и сети

Отражения меняют ориентацию, таким образом, как двумерные фигуры, трехмерные фигуры могут также быть прямо конгруэнтным или противоположно конгруэнтным .Это особенно важно в органической химии, где ориентация из четырех связей вокруг углерода (тетраэдр) имеет решающее значение для жизни. Видеть это ссылка для получения дополнительной информации (загрузить плагин звонка). Я думал, что в последние годы была распространена диетическая добавка с обоими изомерами, и много людей погибло, но триптофан похоже, в конечном итоге возникла другая (димерная) проблема.

Архитекторы часто рисуют масштабные виды или планы зданий.Некоторые могут назвать эти отметок . Этот сайт есть сети для многих твердых тел и другие лакомые кусочки.

Сетка представляет собой двумерную фигуру, которую можно складывать на сегменты
или изогнутые на своих границах в трехмерную поверхность.

Раскраска карты

http://www.ams.org/notices/199807/thomas.pdf Сколько цветов необходимо и сколько цветов достаточно, чтобы раскрасить любую карту на плоскости? На сфере (4)? На ленте Мёбиуса (6)? На торе (7)? Карты с границами, состоящими только из прямых или окружностей может понадобиться еще меньше цветов! (Смотрите рисунок справа.) За исключением плоскости / сферы, эти вопросы были легко ответить.

Подобно сети, карта представляет собой двумерное приближение для трехмерной фигуры. Когда это карта земли, часто встречаются различные искажения. Если вы взяли глобус и разрезали его примерно через каждые 15 ° долготы, в результате пробок (см. рисунок слева) можно было уложить горизонтально. Это было бы довольно точно, но довольно неудобно — разные части одна и та же страна будет на разных глубинах и фактической форме этих стран трудно увидеть.Исторически сложилось так, что проекция Меркатора , созданная обычно используется фламандский картограф 1569 года. Особенно искажены земельные участки вблизи полюсов, что приводит к Африка (11 миллионов миль ²) размером с Гренландию (менее 1 миллиона миль ²). Это происходит потому, что проекция Меркатора на самом деле является чистой для цилиндра, а не для сферы. Преобразование можно создать, расширив лучи из центра земли на боковую грань цилиндра.Как указано выше, это преобразование не является изометрией. Однако он сохраняет промежуточность и коллинеарность, по линиям долготы и широты. Таким образом, четыре направления (север, юг, восток и запад) находятся на перпендикулярных линиях.

Изучив карты, Фрэнсис Гатри в 1852 году предположил, что любой карту на сфере или плоскости можно выделить / раскрасить всего четыре цвета. Легко видеть, что необходимы четыре цвета (см. Справа).Однако доказательство достаточности части было завершено только в 1976 году. Даже тогда доказательство, представленное Haken и Appel , было спорным. уже много лет. Споры возникли из-за того, что они использовали компьютер чтобы доказать, что нужны были только четыре цвета для каждого из 1952 типов возможных карт. Проблема была встроена в теория графов перед этим анализом.

Теорема о четырех цветах . Предположим, что области, имеющие общую границу некоторой длины, должны иметь различные цвета.Тогда любая карта регионов на плоскости или сфере может быть раскрашенным таким образом, чтобы нужно было всего четыре цвета. Предположено Гутри в 1852 году; доказано Хакеном и Аппелем в 1976 г.

Ниже представлен раздаточный материал для домашнего задания 9.8 №26. (Где-то добавить угол наклона / наклон и график двугранных углов.)

Учебное пособие — стр. 10 Лайновая бумага. Словарь. Изометрический рисунок трехмерного объекта показывает три стороны фигуры с углового вида.Рабочая тетрадь.

Презентация на тему: «Учебник — страница 10 Лайновая бумага. Словарь. Изометрический рисунок трехмерного объекта показывает три стороны фигуры с углового обзора. Рабочая тетрадь.» — стенограмма презентации:

1 Учебник — страница 10 Лайновая бумага

2 Словарь. Изометрический рисунок трехмерного объекта показывает три стороны фигуры с углового вида.Рабочая тетрадь — страница 4

3 Учебник — страница 10 Точечная бумага

4 Словарь терминов — страница 4 Орфографический рисунок трехмерного объекта показывает вид сверху, вид спереди и вид справа

5 Учебник — страница 11 Точечная бумага

6 Сделайте орфографический рисунок изометрического рисунка ниже.Ортографические рисунки сглаживают глубину фигуры. Орфографический чертеж показывает три вида. Поскольку ни один край изометрического чертежа не скрыт на виде сверху, спереди и справа, все линии сплошные. Чертежи для быстрой проверки, цепи и другие модели УРОК 1-2 Рабочая тетрадь — стр. 4

8 Словарь терминов — страница 4 Сеть — это двухмерный узор, который можно сложить, чтобы образовать трехмерный

10 Нарисуйте сетку для фигуры с квадратным основанием и четырьмя гранями равнобедренного треугольника.Обозначьте сетку ее размерами. Думайте о сторонах квадратного основания как о петлях и «разверните» фигуру по этим краям, чтобы сформировать сеть. Основание каждой из четырех граней равнобедренного треугольника является стороной квадрата. Чертежи, сети и другие модели УРОК 1-2 Рабочая тетрадь быстрой проверки — стр. 4

определение рисунка и синонимов рисунка (английский)

FigureFig «ure (fĭg» �r; 135), n. [F., рисунок, L. figura; сродни пальцу по форме, форме, притворству. См. Feign.]
1. Форма чего-либо; форма; контур; внешний вид.

У цветов все изящные фигуры. Бекон.

2. Изображение любой формы, в том числе рисунком, росписью, лепкой, резьбой, вышивкой и др .; особенно изображение человеческого тела; как, фигура из бронзы; фигура, вырезанная из мрамора.

Монета с изображением ангела. Шак.

3. Рисунок на ткани, бумаге или другом промышленном изделии; дизайн, выполненный на ткани; как, кисея была красивой фигуры.

4. (Геом.) Диаграмма или рисунок, сделанный для представления величины или соотношения двух или более величин; поверхность или пространство, закрытые со всех сторон; — называется поверхностным, если оно ограничено линиями, и твердым, если оно ограничено поверхностями; любое расположение, состоящее из точек, линий, углов, поверхностей и т. д.

5. Внешний вид или впечатление, производимое поведением или карьерой человека; как жаль цифра.

Я там нарисовал какую-то фигуру. Драйден.

Господа лучшие фигуры в округе. Черный камень.

6. Отличный внешний вид; великолепие; заметное изображение; великолепие; шоу.

Чтобы он жил в фигуре и снисходительности. Закон.

7. Знак или символ, представляющий число; числительное; цифра; as, 1, 2,3 и т. д.

8. Значение, выраженное цифрами; цена; поскольку, товары оцениваются или продаются по заниженной цене.[В разговоре.]

Девятнадцать тысяч в год — это самый низкий показатель. Теккерей.

9. Человек, вещь или действие, воспринимаемое как аналог другого лица, вещи или действия, которое, таким образом, становится типом или представителем.

Кто есть фигура Грядущего. ПЗУ. v. 14.

10. (Rhet.) Способ выражения абстрактных или нематериальных идей словами, предполагающими картинки или образы из физического мира; изобразительный язык; троп; отсюда любое отклонение от самой простой формы заявления.Также называется фигурой речи.

Изображать воображение под фигурой крыла. Маколей.

11. (Логика) Форма силлогизма относительно взаимного расположения среднего члена.

12. (Танец) Любой из нескольких стандартных шагов или движений танцора.

13. (Астрол.) Гороскоп; диаграмма аспектов астрологических домов. Джонсон.

14. (Музыка) (а) Любая короткая последовательность нот в виде мелодии или группы аккордов, производящих единое законченное и отчетливое впечатление.Роща.

(b) форма мелодии или аккомпанемента, поддерживаемая в звуке или отрывке; музыкальная фраза или мотив; витиеватое украшение.

☞ Цифры часто пишутся на нотном стане для обозначения вида меры. Обычно они представлены в виде дроби, верхнее число показывает, сколько нот того типа, который указан нижним, содержится в одном такте или такте. Таким образом, 2/4 означает, что такт содержит две четвертные ноты. Для этой цели используются следующие основные фигуры: —2/22/42/8 4/22/44/8 3/23/43/8 6/46/46/8

Фигурка Академии, Погашенные фигуры, Lay рисунок и др.См. В разделе «Академия», «Отмена», «Лей» и т. Д. — Фигура заклинателя или Фигура метателя, астролог. «Этот заклинатель фигур». Милтон. — Подбрасывание фигур, практика астрологии. — Узел в форме восьмерки, узел в форме фигуры 8. См. Рис. под узлом. — Рисунок рисунка, изображение человеческой фигуры или акт или искусство изображения человеческой фигуры. — Фигурный камень (мин.), Агальматолит. — Фигурное плетение, искусство или процесс плетения фигурных тканей. — Вырезать фигуру, сделать показ. [Разговор.] Сэр В.Скотт.

Периметр — длина границы двухмерной фигуры.

43 Периметр и Площадь

43 Периметр и площадь Периметры фигур встречаются в реальных жизненных ситуациях.Например, кто-то может захотеть узнать, какой длины забор будет окружать прямоугольное поле. В этом разделе мы изучим

Дополнительная информация Периметр, площадь и объем
Периметр, площадь и объем Периметр обычных геометрических фигур Периметр геометрической фигуры определяется как расстояние вокруг внешней стороны фигуры. Периметр рассчитывается путем сложения всех
Дополнительная информация Глоссарий по алгебре и геометрии.Угол 90
lgebra Геометрия Глоссарий 1) острый угол угол меньше 90 острый угол 90 угол 2) острый треугольник треугольник, все углы которого меньше 90 3) смежные углы, углы, имеющие общий отрезок Пример:
Дополнительная информация Площадь. Обзор области. Определить: Площадь:
Определить: Область: Обзор области Воздушный змей: Параллелограмм: Прямоугольник: Ромб: Квадрат: Трапеция: Постулаты / Теоремы: У каждой закрытой области есть область.Если замкнутые фигуры совпадают, то их площади равны.
Дополнительная информация Примечания к геометрии ПЕРИМЕТР И ПЛОЩАДЬ
Периметр и площадь Страница 1 из 57 ПЕРИМЕТР И ПЛОЩАДЬ Цели: После завершения этого раздела вы должны быть в состоянии сделать следующее: Вычислить площадь заданных геометрических фигур. Рассчитываем периметр
Дополнительная информация Периметр.14 футов. 5 футов. 11 футов.
Периметр Периметр геометрической фигуры — это расстояние вокруг фигуры. Периметр можно рассматривать как обход фигуры, отслеживая пройденное расстояние. Определить
Дополнительная информация Геометрия и измерения
Учащийся сможет: Геометрия и измерение 1. Продемонстрировать понимание принципов геометрии, измерения и операций с использованием измерений. Использовать американскую систему измерения для
. Дополнительная информация 2006 Геометрия Форма A Страница 1
2006 Форма Геометрии Страница 1 1.Гипотенуза прямоугольного треугольника имеет длину 12 дюймов, а один из острых углов составляет 30 градусов. Длина более короткой части должна быть: () 4 3 дюйма () 6 3 дюйма () 5 дюймов
Дополнительная информация ПЛОЩАДЬ И ОБЪЕМ ПОВЕРХНОСТИ
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ В этом модуле мы научимся определять площадь поверхности и объем следующих трехмерных тел :. Призмы. Пирамиды 3. Цилиндры 4. Конусы Предполагается, что у читателя
Дополнительная информация 10-3 Площадь параллелограммов
0-3 Площадь параллелограммов ОСНОВНАЯ ИДЕЯ Найдите площади параллелограммов.Основной учебный план штата Нью-Йорк 6.A.6 Оценить формулы для заданных входных значений (окружность, площадь, объем, расстояние, температура, процент,
Дополнительная информация 9 Площадь, периметр и объем
9 Площадь, периметр и объем 9.1 Двумерные фигуры В следующей таблице приведены названия некоторых двухмерных фигур. В этом разделе мы рассмотрим свойства некоторых из этих фигур. Прямоугольник Все углы прямые
Дополнительная информация Пицца! Пицца! Оценка
Пицца! Пицца! Оценка 1.Местный ресторан-пиццерия отправляет пиццу в старшую двенадцатую школу в картонных коробках. Если толщина пиццы один дюйм, каков объем цилиндрической транспортной коробки для
? Дополнительная информация Окружность круга
Окружность круга Круг — это фигура, все точки которой находятся на одинаковом расстоянии от центра. Он назван центром. Круг слева называется кругом A, так как центр находится в точке A.Если
Дополнительная информация Приложения для треугольников
Не в масштабе Приложения для треугольников 1. 36 дюймов 40 дюймов 33 дюймов 1188 дюймов 2 69 дюймов 2 138 дюймов 2 1440 дюймов 2 2. 188 дюймов 2 278 дюймов 2 322 дюйма 2 ни один из Находят площадь параллелограмма с заданными
Дополнительная информация Определение объема прямоугольных призм
MA.FL.7.G.2.1 Обоснование и применение формул для площади поверхности и объема пирамид, призм, цилиндров и конусов. MA.7.G.2.2 Используйте формулы для определения площади поверхности и объема трехмерных составных форм.
Дополнительная информация Как найти площадь формы
9 Областей и периметров Это наш следующий ключевой блок геометрии. В нем мы резюмируем некоторые концепции, с которыми мы встречались раньше. Мы также начнем развивать более алгебраический подход к поиску площадей и периметров.
Дополнительная информация Площадь и окружность
4.4 Площадь и окружность 4.4 ЦЕЛИ 1. Используйте p, чтобы найти длину окружности 2. Используйте p, чтобы найти площадь круга 3. Найдите площадь параллелограмма 4. Найдите площадь треугольника 5. Преобразуйте
Дополнительная информация Расчет периметра
Расчет периметра и формулы площади — это уравнения, используемые для конкретных расчетов.Общие формулы (уравнения) включают: P = 2l + 2w периметр прямоугольника A = l + w площадь квадрата или прямоугольника
Дополнительная информация Краткая справочная электронная книга
Этот файл распространяется БЕСПЛАТНО издателем Quick Reference Handbooks и автором. Электронная книга «Краткий справочник» Щелкните «Содержание» или «Указатель» на левой панели, чтобы выбрать тему. Математические факты перечислены
Дополнительная информация 1 Введение в основную геометрию
1 Введение в основную геометрию 1.1 Евклидова геометрия и аксиоматические системы 1.1.1 Точки, линии и отрезки прямых Геометрия — одна из старейших областей математики. Слово геометрия в греческом
Дополнительная информация Геометрия 2D-форм
Название: Геометрия двумерных фигур Ответьте на следующие вопросы в своей классной рабочей тетради: 1. Дайте определения каждой из следующих форм и нарисуйте каждую из них: а) равносторонний треугольник б) равнобедренный
Дополнительная информация 16 кругов и цилиндров
16 кругов и цилиндров 16.1 Введение в круги В этом разделе мы рассматриваем круг, глядя на рисование кругов и линий, разделяющих круги на разные части. Аккорда соединяет любые два
Дополнительная информация 2014 2015 Обзор экзамена по геометрии B
Семестр Eam Review 014 015 Geometr B Eam Review Примечания для студента: Этот обзор готовит нас к семестру B Geometr Eam. Команда будет охватывать разделы 3, 4 и 5 учебной программы Geometr.Емкость состоит из
человек. Дополнительная информация История измерений в США
РАЗДЕЛ 11.1. ЛИНЕЙНОЕ ИЗМЕРЕНИЕ. История измерения в США. Английская система измерения выросла из творческого подхода, который люди измеряли сами. Знакомые предметы и части тела были
Дополнительная информация Окружность и площадь круга
Обзор Математические концепции Материалы Учащиеся узнают, как вычислить число пи (π) в виде отношения.Студенты также изучают окружность и площадь круга с помощью формул. числа и операции TI-30XS MultiView двумерный
Дополнительная информация Урок 21. Круги. Цели
Имя учащегося: Дата: Имя контактного лица: Номер телефона: Урок 1 Круги Цели Понять концепции радиуса и диаметра. Определить длину окружности круга, учитывая диаметр или радиус. Определить
. Дополнительная информация Подумайте об этой ситуации
Подумайте об этой ситуации. Популярной игрой, которую проводят на ярмарках или вечеринках, является конкурс по угадыванию мармеладов.Кто-то наполняет банку или другой большой прозрачный контейнер известным количеством мармеладов и
Дополнительная информация Пакет обзора формулы MCA
Пакет обзора формул MCA 1 3 4 5 6 7 Математический план MCA-II / BHS Страница 1 из 15 Copyright 005 Клод Паради 8 9 10 1 11 13 14 15 16 17 18 19 0 1 3 4 5 6 7 30 8 9 План математики MCA-II / BHS, стр. Из 15
Дополнительная информация План урока по объему цилиндра
План урока по объему цилиндра. Демонстрация концепции / принципа: на этом уроке будет продемонстрирована связь между диаметром круга и его окружностью, а также влияние на площадь.Самый простой
Дополнительная информация поверхности, 569-571, 576-577, 578-581 треугольника, 548 Ассоциативное свойство сложения, 12, 331 умножения, 18, 433
Абсолютное значение и арифметика, 730-733 определены, 730 Острый угол, 477 Острый треугольник, 497 Дополнение, 12 Дополнительное ассоциативное свойство, (см. Коммутативное свойство), переносящее, 11, 92 коммутативное свойство
частей трехмерных фигур
В геометрии трехмерная фигура — это сплошная фигура, предмет или форма с тремя измерениями — длиной, шириной и высотой.В отличие от двухмерных фигур, трехмерные имеют толщину или глубину.
Атрибуты трехмерной фигуры — это грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.
Ниже приведены части трехмерной фигуры.
Грани:
Плоские поверхности трехмерных фигур называются гранями.
Кромка:
Сегмент линии, на котором встречаются две грани, называется ребром.
Вершина:
Вершина — это точка, где встречаются 3 ребра.
Пример 1:
Назовите следующую трехмерную фигуру. Также найдите количество граней, ребер и вершин.
Решение:
Название формы = Треугольная пирамида
Грани:
Наблюдая за фигурой выше, мы узнаем, что есть четыре грани.
Имя каждой грани:
Грань 1 = ABD
Грань 2 = ABC
Грань 3 = BCD
Грань 4 = ACD
Края:
Края — это прямые линии, используемые для рисования изображения.
Чтобы нарисовать треугольную пирамиду выше, мы использовали 6 граней. Это
AC, AB, BC, BD, CD и AD.
Вершины:
Вершины — это углы, где встречаются 3 ребра.
Здесь стороны AC, AB и AD пересекаются в точке A. Итак, «A» — одна из вершин данной треугольной пирамиды. Точно так же ребра — это B, C и D.
Итак, данная треугольная пирамида имеет 4 грани, 6 ребер и 4 вершины.
Пример 2:
Назовите следующую трехмерную фигуру.Также найдите количество граней, ребер и вершин.
Решение:
Имя формы = Cube
Faces:
Наблюдая за приведенным выше рисунком, мы узнаем, что существует шесть граней.
Имя каждой грани:
Лицевая сторона 1 = ABCD
Лицевая сторона 2 = ACEF
Лицевая сторона 3 = CDEF
Лицевая сторона 4 = BDHG
Лицевая сторона 5 = ABEH (Назад)
Лицевая сторона 6 = CDFG (Передняя)
Края:
Края — это прямые линии, используемые для рисования изображения.Здесь мы использовали 12 прямых линий, чтобы нарисовать куб.
AB, AC, CD, BD, AE, CF, EF, FG, EH, GH, DG, BH
Вершины:
Вершины — это углы, где встречаются 3 ребра.
Вершины: A, B, C, D, E, F, G, H.
Итак, данный куб имеет 6 граней, 12 ребер и 8 вершин.
Пример 3:
Назовите следующую трехмерную фигуру.Также найдите количество граней, ребер и вершин.
Решение:
Название формы = Пятиугольная пирамида
Грани:
Наблюдая за приведенным выше рисунком, мы узнаем, что существует шесть граней.
Имя каждой грани:
Сторона 1 = ABF
Сторона 2 = AFE
Сторона 3 = AED
Сторона 4 = ACD
Сторона 5 = ABC
Сторона 6 = BCDEF (основа)
Края:
Края — это прямые линии, используемые для рисования изображения.Здесь мы использовали 10 прямых линий, чтобы нарисовать пятиугольную призму.
AB, AF, AC, AD, AE, BF, BC, CD, DE, EF
Вершины:
Вершины — это углы, где встречаются 3 ребра.
Вершины: A, B, C, D, E, F.
Итак, у данной пятиугольной пирамиды 6 граней, 10 ребер и 6 вершин.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
[email protected]
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебраные задачи со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
Word по типам ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Разметка и разметка Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных дробях
Одношаговые задачи о словах с уравнениями
Проблемы с линейными неравенствами
Соотношение и пропорции Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами на постоянной скорости
Проблемы со словами на средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времени
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Домен и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di видение
L.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
.